Услуги

Марки

Шоссе

Техцентры на карте

Новости

Архив новостей

Вопрос-ответ

Архив ответов

III Таблица дифференциалов. Таблица дифференциал

III Таблица дифференциалов

Так как дифференциал dyлишь множителемdxотличается от производной, то по таблице производных легко составить таблицу дифференциалов.

1. ,,.

2. ,.

3. ,.

4. . 5..

6. . 7..

8. . 9..

10. . 11..

Также легко получить формулы для дифференциалов суммы, разности, произведения и частного функций:

а)

б)

в)

Отметим, что в таблице дифференциалов переменная xможет быть как независимой, так и некоторой функцией. В таблице же производных (§6)x– это только независимая переменная.

Замечание.Формула для дифференциала функции, а именно:

позволяет написать формулу, выражающую производную функции через дифференциалы dxиdy:

При этом такая формула сохраняет силу, по какой бы независимой переменной ни были вычислены dxиdy. Эта формула позволяет легко запоминать (но не доказывать!) некоторые правила дифференцирования:

для сложной функции

;

для обратной функции

;

для функции, заданной параметрически

§8. Производные высших порядков

I Определение и обозначения

Если функция дифференцируема на некотором промежутке, то её производнаясама является функцией, определенной на этом промежутке. Следовательно, по отношению к ней можно ставить вопрос о существовании и нахождении производной. Если она существует, то её называют второй производной (или производной 2гопорядка), и обозначают одним из символов

Аналогично, если существует производная от второй производной, то её называют третьей производной и обозначают, например, .

Вообще, производной n-го порядка называют производную от производной (n–1)-го порядка и обозначают. Итак, по определению

II Производные некоторых функций

1. y=sinx, y=cosx

Первые производные этих функций и формулы приведенияпозволяют методом математической индукции получить выражения для производныхn-го порядка:

2. y=x

Если , то, последовательно дифференцируя, получим,, и вообще:

Если же показатель степени натуральный, то:

3. y=ax

, в частности,,.

4. y=lnx

III Некоторые правила

Очевидно, что и. Для производной

n-го порядка от произведения функций имеется т.н. формула Лейбница. Приведем ее без доказательства:

, где.

Заметим, что под производной нулевого порядка принято понимать саму

функцию: .

IV Функция, заданная параметрически

Пусть функция задана параметрическими уравнениями

Её первая производная – это также функция, заданная параметрически:

Тогда

Пример.Дляпервая производная имеет видТогдаи вторая производная такова:

V Функция, заданная неявно

Повторное дифференцирование такой функции покажем на примере:

Тогда по определению:

Остается подставить в последнее выражение значение :

Полученное выражение можно упростить, используя само уравнение:

Тема ОСНОВНЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ

Лекция 10

§1. Необходимое условие экстремума

Рассмотрим функцию , определенную на промежутке, и пусть точка–внутренняяточка промежутка:.

Определение 1.Точканазывается точкой (локального) максимума функции, если существует окрестность этой точки, в которой (при) выполняется неравенство. Другими словами для малых приращений аргументаприращение функции.

Определение 2.Точканазывается точкой (локального) минимума функции, если существует окрестность этой точки, в которой (при) выполняется неравенство. Другими словамипри малых.

Точки максимума и минимума называются точками экстремума. Их можно характеризовать следующим образом: приращение функции в точке экстремума имеет постоянный знак, не зависящий от знака (еслидостаточно мало).

Теорема Ферма.Если функциядифференцируема в точкеи имеет в этой точке локальный экстремум, то.

Доказательство.Дифференцируемость означает существование конечного предела

Для этого предела имеется три возможности: 1) ; 2);

3) . Предположим, что. Тогда для близких к нулюразностное отношение. Если же, то и(для малых). В обоих случаях знакзависит от знака. Но по условию теоремы– это точка экстремума, значит, знакне зависит от знака. Это противоречие означает, чтоне может быть ни положительным, ни отрицательным. Остается последняя возможность:.

Замечание 1.Эта теорема имеет простой геометрический смысл: если в точке графика функции, которой соответствует экстремум функции, существует касательная к графику, то эта касательная параллельная осиOx.

Замечание 2.Сформулированное в теореме условиеявляется необходимым, но не достаточным. Например, функцияимеет производную, которая обращается в ноль в точке. Однако,

Выражение в скобках всегда положительно, как неполный квадрат суммы. Следовательно, и в точкенет экстремума.

studfiles.net

III Таблица дифференциалов

1. ,,.

2. ,.

3. ,.

4. . 5..

6. . 7..

8. . 9..

10. . 11..

Также легко получить формулы для дифференциалов суммы, разности, произведения и частного функций:

а)

б)

в)

Замечание.Формула для дифференциала функции, а именно:

позволяет написать формулу, выражающую производную функции через дифференциалы dxиdy:

для сложной функции

;

для обратной функции

;

для функции, заданной параметрически

§8. Производные высших порядков

I Определение и обозначения

II Производные некоторых функций

1. y=sinx, y=cosx

2. y=x

Если , то, последовательно дифференцируя, получим,, и вообще:

Если же показатель степени натуральный, то:

3. y=ax

, в частности,,.

4. y=lnx

III Некоторые правила

Очевидно, что и. Для производной

n-го порядка от произведения функций имеется т.н. формула Лейбница. Приведем ее без доказательства:

, где.

Заметим, что под производной нулевого порядка принято понимать саму

функцию: .

IV Функция, заданная параметрически

Пусть функция задана параметрическими уравнениями

Её первая производная – это также функция, заданная параметрически:

Тогда

Пример.Дляпервая производная имеет видТогдаи вторая производная такова:

V Функция, заданная неявно

Повторное дифференцирование такой функции покажем на примере:

Тогда по определению:

Остается подставить в последнее выражение значение :

Полученное выражение можно упростить, используя само уравнение:

Тема ОСНОВНЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ

Лекция 10

§1. Необходимое условие экстремума

Рассмотрим функцию , определенную на промежутке, и пусть точка–внутренняяточка промежутка:.

Теорема Ферма.Если функциядифференцируема в точкеи имеет в этой точке локальный экстремум, то.

Доказательство.Дифференцируемость означает существование конечного предела

Для этого предела имеется три возможности: 1) ; 2);

Выражение в скобках всегда положительно, как неполный квадрат суммы. Следовательно, и в точкенет экстремума.

studfiles.net

Свойства дифференциалов, все формулы и примеры

1. Дифференциал константы равен нулю:

$dC = 0\text{ },\text{ } C = \text{const}$

2. Дифференциал суммы функций равен сумме дифференциалов слагаемых:

$d(u(x) + v(x)) = du(x) + dv(x)$

Следствие. Если две функции отличаются на константу, то их дифференциалы равны:

$v(x) = u(x) + C \text{ } \Rightarrow \text{ } dv(x) = d(u(x) + C) = du(x)\text{ },\text{ } C = \text{const}$

3. Дифференциал произведения двух функций равен произведению дифференциала первой функции на вторую плюс первая функция на дифференциал второй:

$d(u(x) \cdot v(x)) = d(u(x)) \cdot v(x) + u(x) \cdot d(v(x))$

Следствие. Постоянный множитель можно выносить за знак дифференциала:

$d(Cu(x)) = Cdu(x)\text{ },\text{ } C = \text{const}$

4. Дифференциал частного двух функций 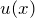u(x) и v(x)

задается формулой:

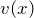
$d \left( \frac{u(x)}{v(x)} \right) = \frac{du(x) \cdot v(x) - u(x) \cdot dv(x)}{(v(x))^2} \text{ },\text{ } v(x) \ne 0$

5. Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной функции на дифференциал аргумента независимо от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Дифференциал функции

Литература.[1], [2], [6], [7], [17].

Понятие дифференциала функции, его геометрический смысл

Пусть функция дифференцируема на отрезке. Производная этой функции в некоторой точкеотрезкаопределяется равенством:. Тогда, по теореме о связи функции, её предела и бесконечно малой функции, можно записать, гдепри, или.

Приращение функции состоит из двух слагаемых, из которых первое есть так называемая главная часть приращения, линейная относительно.

Дифференциалом функции в точкеназывается главная часть её приращения, которая равна произведению производной функции на приращение аргумента, и обозначаетсяили:.

Дифференциал называют также дифференциалом первого порядка.

Дифференциал независимой переменной равен приращению этой переменной: и тогда, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Пример 1.Найти дифференциал функции.

Решение:По формуленаходим

Основные теоремы о дифференциалах. Таблица дифференциалов.

Теорема 1. Дифференциал суммы, произведения и частного двух дифференцируемых функций определяется формулами:

Теорема 2. Дифференциал сложной функции равен произведению производной этой функции по промежуточной переменной на дифференциал этой промежуточной переменной

Таблица дифференциалов

Применение дифференциала в приближенных вычислениях

Пример 2. Вычислить приближенно.

Решение. Рассмотрим функциюf(x)=arctg x.

По формуле имеем:

т.е.

Так как , то прииполучаем:

Вопросы для самопроверки

1.Что называется дифференциалом функции, каков его геометрический смысл?

2. Сформулируйте основные свойства дифференциала функции.

3. Чем отличается дифференциал функции от ее приращения?

4. Укажите формулу для приближенного вычисления значений функции с помощью дифференциала.

5. Что называется дифференциалом второго порядка от данной функции?

Приложения производной

Литература.[1], [2], [6], [7], [17].

Применение производной к вычислению пределов.

Кроме элементарных способов, весьма эффективным средством для нахождения предела функции в тех случаях, когда аргумент неограниченно возрастает или стремится к значению, которое не входит в область определения функции, является правило Лопиталя.

Теорема.Предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных, если он существует или равен бесконечности.

Итак, если имеются неопределенности вида или, то

Обращаем внимание, что в правой части формулы берется отношение производных, а не производная отношения.

Пример.Найти: а)б)в)

Решение.а) Имеем неопределенность вида. Применяя правило Лопиталя, получим:

б)

Неопределенность вида по-прежнему сохраняется. Применим правило Лопиталя еще раз:

в) Имеем неопределенность вида . Переписываем данное выражение в виде

получим неопределенность вида . Применяя правило Лопиталя, получим

Применение производной к исследованию функций Возрастание и убывание функций

При изучении поведения функции в зависимости от изменения независимой переменной обычно предполагается, что во всей области определения функции независимая переменная изменяется монотонно возрастая, т.е. что каждое следующее ее значение больше предыдущего.

Если при этом последовательные значения функции также возрастают, то и функция называется возрастающей, а если они убывают, то и функция называется убывающей.

Некоторые функции во всей своей области определения изменяются монотонно – только возрастают или только убывают (например ).

Многие функции изменяются не монотонно. В одних интервалах изменения независимой переменной они возрастают, а в других интервалах убывают (например, sinx,cosx).

Возрастание и убывание функции характеризуется значением ее производной: если в некотором интервале>0, то функция возрастает, а если<0, то функция убывает в этом интервале.

studfiles.net

6.9. Таблица производных и дифференциалов.

Соберём полученные в разделах 6.2, 6.3, 6.5 выражения для производных и следующие из них выражения для дифференциалов в одну таблицу:

№	y(x)	y'(x)	dy	№	y(x)	y'(x)	dy
1	y = C	0	0	10
2	у = ха	a ха-1	a ха-1dx	11
3				12
3a				14
4				15
4a				16
5				17
6				18
7				19
8				20
9				21

6.10. Производные функций, заданных параметрически и неявно.

6.10.1. Производные функций, заданных параметрически. Пусть зависимость у от х задана через параметр t: , обе эти функции дифференцируемы, и для первой из них существует обратная функция . Тогда явная зависимость у от х выражается формулой. Находим производную: . Здесь мы воспользовались результатами разделов 6.5.5. Производная сложной функции и 6.3. Производная обратной функции. То же выражение можно получить из 6.8.2. Инвариантности формы первого дифференциала: .

Примеры:

. Тогда . В этом примере легко получить явную зависимость у от х: . Подставим сюда зависимость х от t: . Как и следовало ожидать, получен тот же результат.
. Тогда .

6.10.2. Производные функций, заданных неявно. Неявным заданием зависимости у от х называется уравнение вида F(x,y) = 0, связывающее эти две переменные. Общая формула для y'(x), следующая из неявного уравнения F(x,y) = 0, включает в себя частные производные, которые мы будем изучать позже; пока приведём несколько примеров, показывающих, как найти производную y'(x) из неявного уравнения.

1. . Дифференцируем это равенство по х, учитывая зависимость у от х (применяя правило дифференцирования сложной функции: ):

. Легко понять, что при этом всегда получится уравнение, линейное относительно y'(x), которое без труда решается: . Производная найдена, она совпадает с полученной в предыдущем разделе (с учётом явного выражения ).

2. . Дифференцируем по х, учитывая зависимость у от х:

Решаем это уравнение относительно y': .

6.11. Производные и дифференциалы высших порядков.

6.11.1. Производные высших порядков. Формула Лейбница. Пусть функция имеет производную y'(x) в каждой точке интервала (а,b). Функция y'(x) тоже может иметь производную в некоторых точках этого интервала. Производная функции y'(x) называется второй производной (или производной второго порядка) функции и обозначается . Функция y''(x) тоже может иметь производную, которая называется третьей производной (или производной третьего порядка) функции и обозначается . Вообще n-ой производной (или производной n-ого порядка) функции называется производная от производной n-1-го порядка (обозначения: ).

Производные высших порядков последовательно вычисляются по уже известным формулам и правилам. Пусть, например, . Тогда , , , и т.д. В некоторых случаях можно получить общее выражение для n-ой производной функции: пусть . Тогда , , , и вообще . Аналогичную формулу можно получить для косинуса. Другой пример: . Если представить эту функцию в виде , то ,, и вообще .

Для высших производных произведения функций справедлива формула Лейбница:

. Эта формула внешне похожа на формулу бинома Ньютона и, также как формула бинома Ньютона, может быть доказана методом математической индукции. Для низших производных:

; ; .

6.11.2. Дифференциалы высших порядков также определяются индуктивно: дифференциалом второго порядка (или вторым дифференциалом) функции называется дифференциал от её первого дифференциала; дифференциалом третьего порядка называется дифференциал от второго дифференциала; и вообще, дифференциалом n-го порядка функции называется дифференциал от её n-1-го дифференциала. При вычислении высших дифференциалов необходимо учитывать, что дифференциал независимой переменной - произвольная и независимая от х величина, которая при дифференцировании рассматривается как постоянная. Поэтому ; ; …., .

6.11.3. Неинвариантность формы старших дифференциалов относительно замены переменной. В разделе 6.8.2. Инвариантность формы первого дифференциала мы доказали, что независимо от того, является ли х независимой переменной, или сама эта переменная х является функцией другой переменной t, формула для нахождения дифференциала первого порядка одна и та же: dy = y'dx. Покажем, что уже второй дифференциал этим свойством не обладает. Если х - независимая переменная, то d 2y = y"dx2. Если x = (t), то d 2y = d(dу) = d(y'хdx) =

= d(y'х)dx + y'хd(dx). Для первого слагаемого вследствие инвариантности формы первого дифференциала d(y'х) = y"ххdx, для второго d(dx) = d 2x, поэтому окончательно d 2y = y"ххdx2+ y'хd 2x, что отличается от случая независимой переменной. Причина этого понятна: если х независимая переменная, то при нахождении второго дифференциала dx рассматривается как независимая от x константа; в случае x = (t) дифференциал dx определяется дифференциалом dt.

6.11.4. Старшие производные функции, заданной параметрически. В разделе 6.10.1. Производные функций, заданных параметрически, для первой производной функции

была получена формула . Если применить эту формулу к функции

то получим: ; аналогично, применяя ту же формулу ко второй производной, получим выражение для третьей производной, и т.д. Так, для функции мы получили . Найдем вторую производную: .

6.11.5. Старшие производные функции, заданной неявно, находятся последовательно, в соответствии с определением старших производных. Так, для неявно заданной зависимости у от х мы получили . Найдём вторую производную: . Дальше можно найти третью и т.д. производные.

studfiles.net

Дифференциал таблица

24. ДИФФЕРЕНЦИАЛ ФУНКЦИИ

24.1. Понятие дифференциала функции

Пусть функция у=ƒ(х) имеет в точке х отличную от нуля производную.

Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать D у/ D х=ƒ'(х)+α, где α→0 при ∆х→0, или ∆у=ƒ'(х)•∆х+α•∆х.

Таким образом, приращение функции ∆у представляет собой сумму двух слагаемых ƒ'(х)•∆х и а•∆х, являющихся бесконечно малыми при ∆x→0. При этом первое слагаемое есть бесконечно малая функция одного порядка с ∆х, так как а второе слагаемое есть бесконечно малая функция более высокого порядка, чем ∆х:

Поэтому первое слагаемое ƒ'(х) · ∆х называют главной частью приращения функции ∆у.

Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):

Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.

Так как у’=х’=1, то, согласно формуле (24.1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.

Поэтому формулу (24.1) можно записать так:

иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.

Из формулы (24.2) следует равенство dy/dx=ƒ'(х). Теперь обозначение

производной dy/dx можно рассматривать как отношение дифференциалов dy и dх.

Найти дифференциал функции ƒ(х)=3x 2 -sin(l+2x).

Решение: По формуле dy=ƒ'(х) dx находим

dy=(3х 2 -sin(l+2x))’dx=(6х-2cos(l+2х))dx.

Найти дифференциал функции

Вычислить dy при х=0, dx=0,1.

Подставив х=0 и dx=0.1, получим

24.2. Геометрический смысл дифференциала функции

Выясним геометрический смысл дифференциала.

Для этого проведем к графику функции у=ƒ(х) в точке М(х, у) касательную МТ и рассмотрим ординату этой касательной для точки х+∆х (см. рис. 138). На рисунке ½ АМ ½ =∆х, |AM1|=∆у. Из прямоугольного треугольника МАВ имеем:

Но, согласно геометрическому смыслу производной, tga=ƒ'(х). Поэтому АВ=ƒ'(х)•∆х.

Сравнивая полученный результат с формулой (24.1), получаем dy=АВ, т. е. дифференциал функции у=ƒ(х) в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получит приращение ∆х.

В этом и состоит геометрический смысл дифференциала.

24.3 Основные теоремы о дифференциалах

Основные теоремы о дифференциалах легко получить, используя связь дифференциала и производной функции (dy=f'(x)dx) и соответствующие теоремы о производных.

Например, так как производная функции у=с равна нулю, то дифференциал постоянной величины равен нулю: dy=с’dx=0•dx=0.

Теорема 24.1. Дифференциал суммы, произведения и частного двух дифференцируемых функций определяются следующими формулами:

Докажем, например, вторую формулу. По определению дифференциала имеем:

d(uv)=(uv) ‘ dx=(uv ‘ +vu ‘ )dx=vu ‘ dx+uv ‘ dx=udv+vdu

Теорема 24.2. Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.

Пусть у=ƒ(u) и u=φ(х) две дифференцируемые функции, образующие сложную функцию у=ƒ(φ(х)). По теореме о производной сложной функции можно написать

Умножив обе части этого равенства на dx, поучаем у’хdx=у’u•u’хdx. Но у’хdx=dy и u’хdx=du. Следовательно, последнее равенство можно переписать так:

Сравнивая формулы dy=у’х•dx и dy=у’u•du, видим, что первый дифференциал функции у=ƒ(х) определяется одной и той же формулой независимо от того, является ли ее аргумент независимой переменной или является функцией другого аргумента.

Это свойство дифференциала называют инвариантностью (неизменностью) формы первого дифференциала.

Формула dy=у’х•dx по внешнему виду совпадает с формулой dy=у’u•du, но между ними есть принципиальное отличие: в первой формуле х — независимая переменная, следовательно, dx=∆х, во второй формуле и есть функция от х, поэтому, вообще говоря, du≠∆u.

С помощью определения дифференциала и основных теорем о дифференциалах легко преобразовать таблицу производных в таблицу дифференциалов.

24.4. Таблица дифференциалов

24.5. Применение дифференциала к приближенным вычислениям

Как уже известно, приращение ∆у функции у=ƒ(х) в точке х можно представить в виде ∆у=ƒ'(х)•∆х+α•∆х, где α→0 при ∆х→0, или ∆у=dy+α•∆х. Отбрасывая бесконечно малую α•∆х более высокого порядка, чем ∆х, получаем приближенное равенство

причем это равенство тем точнее, чем меньше ∆х.

Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.

Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (24.3) широко применяется в вычислительной практике.

Найти приближенное значение приращения функции у=х 3 -2х+1 при х=2 и ∆х=0,001.

Посмотрим, какую погрешность допустили, вычислив дифференциал функции вместо ее приращения. Для этого найдем ∆у:

Абсолютная погрешность приближения равна

Подставляя в равенство (24.3) значения ∆у и dy, получим

Формула (24.4) используется для вычислений приближенных значений функций.

Вычислить приближенно arctg(1,05).

Решение: Рассмотрим функцию ƒ(х)=arctgx. По формуле (24.4) имеем:

Так как х+∆х=1,05, то при х=1 и ∆х=0,05 получаем:

Можно показать, что абсолютная погрешность формулы (24.4) не превышает величины М•(∆х) 2 , где М — наибольшее значение |ƒ"(х)| на сегменте [х,х+∆х].

Какой путь пройдет тело при свободном падении на Луне за 10,04 с от начала падения. Уравнение свободного падения тела

Решение: Требуется найти H(10,04). Воспользуемся приближенной формулой (ΔH≈dH)

Задача (для самостоятельного решения). Тело массой m=20 кг движется со скоростью ν=10,02 м/с. Вычислить приближенно кинетическую энергию тела

24.6. Дифференциалы высших порядков

Пусть у=ƒ(х) дифференцируемая функция, а ее аргумент х — независимая переменная. Тогда ее первый дифференциал dy=ƒ'(х)dx есть также функция х, можно найти дифференциал этой функции.

Дифференциал от дифференциала функции у=ƒ(х) называется ее вторым дифференциалом (или дифференциалом второго порядка) и обозначается d 2 y или d 2 ƒ(х).

Итак, по определению d 2 y=d(dy). Найдем выражение второго дифференциала функции у=ƒ(х).

Так как dx=∆х не зависит от х, то при дифференцировании считаем dx постоянным:

Здесь dx 2 обозначает (dx) 2 .

Аналогично определяется и находится дифференциал третьего порядка

И, вообще, дифференциал n-го порядка есть дифференциал от дифференциала (n-1)-го порядка: d n y=d(d n-l y)=f (n) (x)(dx) n .

Отсюда находим, что , В частности, при n=1,2,3

т. е. производную функции можно рассматривать как отношение ее дифференциала соответствующего порядка к соответствующей степени дифференциала независимой переменной.

Отметим, что все приведенные выше формулы справедливы только, если х — независимая переменная. Если же функцию у=ƒ(х), где х — функция от кαкой-mo другой независимой переменной, то дифференциалы второго и выше порядков не обладают свойством инвариантности формы и вычисляются по другим формулам. Покажем это на примере дифференциала второго порядка.

Используя формулу дифференциала произведения (d(uv)=vdu+udv), получаем:

Сравнивая формулы (24.5) и (24.6), убеждаемся, что в случае сложной функции формула дифференциала второго порядка изменяется: появляется второе слагаемое ƒ'(х)•d 2 х.

Ясно, что если х — независимая переменная, то

и формула (24.6) переходит в формулу (24.5).

Найти d 2 y, если у=е 3х и х — независимая переменная.

Решение: Так как у’=3е 3х , у"=9e 3х , то по формуле (24.5) имеем d 2 y=9e 3x dx 2 .

Найти d 2 y, если у=х 2 и х=t 3 +1и t— независимая переменная.

Решение: Используем формулу (24.6): так как

у’=2х, у"=2, dx=3t 2 dt, d 2 x=6tdt 2 ,

то d 2 y=2dx 2 +2x•6tdt 2 =2(3t 2 dt) 2 +2(t 3 +1)6tdt 2 =18t 4 dt 2 +12t 4 dt 2 +12tdt 2 =(30t 4 +12t)dt 2

Другое решение: у=х 2 , х=t 3 +1. Следовательно, у=(t 3 +1) 2 . Тогда по формуле (24.5)

tradesmarter.ru

Дифференциал таблица

Понятие и геометрический смысл дифференциала

Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.

Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).

Это записывается так:

Геометрический смысл дифференциала. Дифференциал функции y = f(x) равен приращению ординаты касательной S, проведённой к графику этой функции в точке M(x, y), при изменении x (аргумента) на величину (см. рисунок).

Почему дифференциал можно использовать в приближенных вычислениях?

Дифференциал, является главной, линейной относительно частью приращения функции, чем меньше , тем большую долю приращения составляет эта часть. В этом можно убедиться, мысленно передвигая перпендикуляр, опущенный из точки P (см. рисунок) к оси Ox, ближе к началу координат. Поэтому при малых значениях (и при ) приращение функции можно приближенно заменить его главной частью , т.е.

О разных формах записи дифференциала

Дифференциал функции в точке x и обозначают

поскольку дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной.

Замечание. Нужно помнить, что если x – исходное значение аргумента, а — наращенное значение, то производная в выражении дифференциала берётся в исходной точке x , в формуле (1) этого не видно из записи.

Дифференциал функции можно записать в другой форме:

Пример 1. Найти дифференциалы функций:

Решение. Применяя формулы дифференцироивания степенной и логарифмической функций из таблицы производных, а также формулу (4), находим:

Найти дифференциалы самостоятельно, а затем посмотреть решения

Пример 2. Найти дифференциал функции

1) выделив линейную часть,

Пример 3. Найти дифференциал функции

Пример 4. Найти дифференциал функции

В основном же задачи на дифференциалы — это более сложные, чем рассмотренные выше для разминки, поэтому стоит посетить страницу с решением задач на дифференциалы сложных функций. Скорее всего, вызывающие у вас трудности задачи именно к таким и относятся.

Свойства дифференциала

В этом и следующем параграфах каждую из функций будем считать дифференцируемой при всех рассматриваемых значениях её аргументов.

Дифференциал обладает свойствами, аналогичными свойствам производной:

(С – постоянная величина) (5)

Формулы (5) – (9) получаются из соответствующих формул для производной умножением обеих частей каждого равенства на .

Применение дифференциала в приближенных вычислениях

Установленное во втором параграфе приближенное равенство

позволяет использовать дифференциал для приближенных вычислений значений функции.

Запишем приближенное равенство более подробно. Так как

Пример 5. Пользуясь понятием дифференциала, вычислить приближенно ln 1,01.

Решение. Число ln 1,01 является одним из значений функции y = ln x . Формула (11) в данном случае примет вид

что является очень хорошим приближением: табличное значение ln 1,01 = 0,0100.

Пример 6. Пользуясь понятием дифференциала, вычислить приближенно

является одним из значений функции

Так как производная этой функции

то формула (11) примет вид

Вычислить приближенно самостоятельно, а затем посмотреть решение

Пример 7. Вычислить приближенно:

Абсолютная и относительная погрешности приближенных вычислений

Пользуясь приближенным значением числа, нужно иметь возможность судить о степени его точности. С этой целью вычисляют его абсолютную и относительную погрешности.

Абсолютная погрешность приближенного числа равна абсолютной величине разности между точным числом и его приближенным значением:

Относительной погрешностью приближенного числа называется отношение абсолютной погрешности этого числа к абсолютной величине соответствующего точного числа:

Если точное число неизвестно, то

Иногда, прежде чем применить формулу (11), требуется предварительно преобразовать исходную величину. Как правило, это делается в двух целях. Во-первых, надо добиться, чтобы величина была достаточно малой по сравнению с , так как чем меньше , тем точнее результат приближенного вычисления. Во-вторых, желательно, чтобы величина вычислялась просто.

Пример 8. Пользуясь понятием дифференциала, вычислить приближенно . Оценить точность полученного результата.

Решение. Рассмотрим функцию

Её производная равна

а формула (11) примет вид

В данном случае было бы нерационально вычислять приближенно следующим образом:

так как значение

не является малым по сравнению со значением производной в точке

Здесь удобно предварительно вынести из под корня некоторое число, например 4/3. Тогда

Умножая на 4/3, находим

Принимая табличное значение корня

за точное число, оценим по формулам (12) и (13) абсолютную и относительную погрешности приближенного значения:

tradesmarter.ru