Большая Энциклопедия Нефти и Газа. Планетарный ряд
Планетарный ряд - Большая Энциклопедия Нефти и Газа, статья, страница 1
Планетарный ряд
Cтраница 1
Планетарный ряд и искомое передаточное число, осуществленное им, назовем основными. [1]
Каждый планетарный ряд в такой коробке передач включается и выключается своими блокировочным фрикционом и тормозным устройством. Фрикционы обеспечивают безударное переключение передач и плавное трогание машины с места. [2]
Опорой планетарного ряда служит водило 3 с сателлитами, установленными в его пазах. Сателлиты вращаются на осях 29, запрессованных в гнездах, расточенных в водиле. Одна беговая дорожка роликов - шлифованная поверхность оси 29, а другая - шлифованная внутренняя поверхность сателлита. [4]
Сателлиты планетарных рядов установлены на игольчатых подшипниках, смазываемых под давлением. Места подвода уплотнены металлическими кольцами. [5]
Одним планетарным рядом каждое из заданных передаточных чисел осуществить нельзя, поэтому получим эти числа при помощи двухрядного механизма. На основании рекомендаций, изложенных в данной работе и табл. 1, можно утверждать, что в одном из этих рядов ведущим является солнечное колесо, тормозом ( Тх) - эпицикл, тормозом T i - водило; ведомым элементом второго ряда является его водило. Варианты двухрядных механизмов изображены на фиг. [6]
Коронная шестерня планетарного ряда приварена к корпусу конечной передачи и является неподвижным элементом планетарного ряда. [7]
Подшипниковые узлы планетарных рядов обычно регулировок не требуют. [8]
Работоспособность шестерни планетарного ряда зависит не только ог точности зубчатого зацепления, но также от точности и шероховатости поверхности торцов и отверстия. [9]
Уравнения связей планетарного ряда, записанные в виде (4.5), справедливы и для двухступенчатой планетарной дифференциальной передачи с двумя центральными колесами. [10]
Смазка деталей планетарных рядов механизмов поворота осуществляется маслом, залитым в картер передачи и разбрызгиваемым вращающимися шестернями. [11]
Полный динамический граф планетарного ряда в рассматриваемом случае имеет вид двухмассовой схемы ( г - р) или ( р - р), рис. 7 в. [12]
ДР состоит из планетарного ряда с двойными сателлитами. Ведущей является коренная шестерня, а ведомая солнечная шестерня соединена с турбинным колесом ГТКМ. [13]
Все коронные шестерни планетарных рядов плавающие без жесткой фиксации. Они служат внутренними барабанами дисковых тормозов. Наружные барабаны тормозов выполнены в виде колец, соединенных жестко в один пакет стяжными болтами. Гидравлические бустера тормозов расположены в расточках колец, имеющих Г - образную форму. [14]
При указанном динамическом представлении планетарного ряда с абсолютно жестко остановленным звеном q для сохранения цепной структуры общей динамической схемы необходимо осуществить приведение координат и упруго-инерционных параметров этой схемы. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
Планетарные зубчатые передачи.
Планетарные зубчатые передачи
Общие сведения о планетарных передачах
Планетарными называют передачи, имеющие зубчатые колеса с подвижными осями. Отличительной особенностью механизмов, включающих планетарную передачу (или передачи), является наличие двух или более степеней свободы. При этом угловая скорость любого звена передачи определяется угловыми скоростями остальных звеньев.
Наибольшее распространение получила простая одинарная планетарная передача (рис. 1), которая состоит из центрального колеса 1 с наружными зубьями, неподвижного центрального колеса 3 с внутренними зубьями; сателлитов 2 – колес с наружными зубьями, зацепляющихся одновременно с колесами 1 и 3 (на рис. 1 число сателлитов с = 3), и водила Н, на котором закреплены оси сателлитов. Водило соединено с тихоходным валом. В планетарной передаче одно колесо неподвижно (соединено с корпусом). Обычно внешнее центральное колесо с внутренними зубьями называют коронным (коронная шестерня или эпицикл), а внутреннее колесо с внешними зубьями – солнечным колесом (солнечная шестерня или солнце).
При неподвижном колесе 3 вращение колеса 1 вызывает вращение сателлитов 2 относительно собственных осей, а обкатывание сателлитов по колесу 3 перемещает их оси и вращает водило Н. Сателлиты таким образом совершают вращение относительно водила и вместе с водилом вокруг центральной оси, с. е. совершают движение, подобное движению планет. Поэтому такие передачи и называют планетарными.
При неподвижном колесе 3 движение передают чаще всего от колеса 1 к водилу Н, можно передавать движение от водила Н к колесу 1.
В планетарных передачах применяют не только цилиндрические, но и конические колеса с прямым или косым зубом.
Если в планетарной передаче сделать подвижными все звенья, т. е. оба колеса и водило, то такую передачу называют дифференциальной. С помощью дифференциального механизма можно суммировать движение двух звеньев на одном или раскладывать движение одного звена на два других. Например, в дифференциале заднего моста автомобиля движение от водила Н передают одновременно колесам 1 и 3, что позволяет при повороте одному колесу вращаться быстрее другого.
***
Разновидности планетарных передач
Существует много различных типов и конструкций планетарных передач. Наиболее широко в машиностроении применяют однорядную планетарную передачу, схема которой показана на рисунке 1. Эта передача конструктивно проста, имеет малые габариты. Находит применение в силовых и вспомогательных приводах. КПД планетарной передачи η = 0,96…0,98 при передаточных числах u = 3…8.
Планетарные механизмы, в составе которых присутствуют одна или несколько планетарных передач подразделяются на однорядные, двухрядные и многорядные. Каждый набор из центральных зубчатых колёс и сателлитов, вращающихся в одной плоскости, образует так называемый планетарный ряд. Простой планетарный механизм с набором одновенцовых сателлитов является однорядным. Простые планетарные механизмы с двухвенцовыми сателлитами являются двухрядными. Сложные планетарные механизмы могут быть двух, трёх, четырёх и даже пятирядными.
Для получения больших передаточных чисел в силовых приводах применяют многоступенчатые планетарные передачи. На рис. 2,а планетарная передача составлена из двух последовательно соединенных однорядных планетарных передач. В этом случае суммарное передаточное число u = u1×u2 ≤ 64, а КПД равен η = η1×η2 = 0,92…0,96.
На рисунке 2, б показана схема планетарной передачи с двухрядным (двухвенцовым) сателлитом, для которой при передаче движения от колеса 1 к водилу Н при n4 = 0 передаточное число определяется из зависимостей:
u = n1/nН = 1 + z2z4/(z1z3).
В этой передаче u = 3…19 при КПД η = 0,95…0,97.
Как упоминалось выше, планетарные передачи, у которых все звенья подвижны, называют дифференциальными или просто дифференциалами.
Неизбежные погрешности изготовления приводят к неравномерному распределению нагрузки между сателлитами. Для выравнивания нагрузки в передачах с тремя сателлитами одно из центральных колес выполняют самоустанавливающимся в радиальном направлении (не имеющим радиальных опор). Для самоустановки сателлитов по неподвижному центральному колесу применяют сферические подшипники качения. Высокие требования предъявляются к прочности и жесткости водила, при этом его масса должна быть минимальной. Обычно водила выполняют литыми или сварными.
***
Достоинства и недостатки планетарных передач
Основными достоинствами планетарных передач являются:
- малые габариты и масса вследствие передачи мощности по нескольким потокам, численно равным количеству сателлитов. При этом нагрузка в каждом зацеплении уменьшается в несколько раз;
- удобство компоновки в машинах благодаря соосности ведущего и ведомого валов;
- работа с меньшим шумом, чем в обычных зубчатых передачах, что обусловлено меньшими размерами колес и замыканием сил в механизме. При симметричном расположении сателлитов силы в передаче взаимно уравновешиваются;
- малые нагрузки на валы и опоры, что упрощает конструкцию опор и снижает потери в них;
- возможность получения больших передаточных чисел при небольшом числе зубчатых колес и малых габаритах передачи.
Не лишены планетарные передачи и недостатков:
- повышенные требования к точности изготовления и монтажа передачи;
- большее количество деталей, в т. ч. подшипников, и более сложная сборка.
***
Область применения планетарных передач
Планетарные передачи применяют как редукторы в силовых передачах и приборах, в коробках передач автомобилей и другой самоходной техники, при этом передаточное число такой КПП может изменяться путем поочередного торможения различных звеньев (например, водила или одного из колес), в дифференциалах автомобилей, тракторов и т. п.
Широкое применение планетарные передачи нашли в автоматических коробках передач автомобилей благодаря удобству управления передаточными числами (переключением передач) и компактности. Можно встретить планетарные передачи и в механизмах привода ведущих колес современных велосипедов. Часто применяют планетарную передачу, совмещенную с электродвигателем (мотор-редуктор, мотор-колесо).
***
Передаточное число планетарных передач
При определение передаточного числа планетарной передачи используют метод остановки водила (метод Виллиса). По этому методу всей планетарной передаче мысленно сообщается дополнительное вращение с частотой вращения водила nН, но в обратном направлении. При этом водило как бы останавливается, а закрепленное колесо освобождается. Получается так называемый обращенный механизм, представляющий собой обычную непланетарную передачу, в которой геометрические оси всех колес неподвижны. Сателлиты при этом становятся промежуточными (паразитными) колесами, т. е. колесами, не влияющими на передаточное число всего механизма. Передаточное число в обращенном механизме определяется как в духступенчатой передаче с одним внешним и вторым внутренним зацеплением.
Здесь существенное значение имеет знак передаточного числа. Передаточное число считают положительным, если в обращенном механизме ведущее и ведомое звенья вращаются в одну сторону, и отрицательным, если в разные стороны. Так, для обращенного механизма передачи по рис. 1 имеем:
u = u1×u2 = (-n1/n2)×(-n2/-n3) = (-z2/z1)×(z3/z2) = - z3/z1,
где z – числа зубьев колес.
В рассматриваемом обращенном механизме знак минус показывает, что колеса 2 и 3 вращаются в обратную сторону по отношению к колесу 1.
В качестве примера определим передаточное число для планетарной передачи, изображенной на рис. 1, при передаче движения от колеса 1 к водилу Н. Мысленная остановка водила в этой передаче равноценна вычитанию его частоты nН из частоты вращения колес. Тогда для обращенного механизма этой передачи имеем:
u’ = (n1 – n2)/(n3 – nН) = - z3/z1,
где (n1 – nН) и (n3 – nН) – частоты вращения колес 1 и 3 относительно водила Н; z1 и z3 – числа зубьев колес 1 и 3.
Для планетарной передачи, у которой колесо 3 закреплено в корпусе неподвижно (n3 = 0), колесо 1 является ведущим, а водило Н – ведомым. Тогда получим передаточное число такой передачи:
(n1 – nН)/(- nН) = - z3/z1;- n1/nН+ 1 = -z3/z1
или
***
Подбор чисел зубьев планетарных передач
В отличие от обычных зубчатых передач расчет планетарных начинают с подбора чисел зубьев на колесах и сателлитах. Рассмотрим последовательность подбора чисел зубьев на примере планетарной передачи, изображенной на рис. 1.
Число зубьев z1 центральной шестерни 1 задают из условия неподрезания ножки зуба: z1 ≥ 17. Принимают z1 = 24 при Н ≤ 350 НВ; z1 = 21 при Н ≤ 52 HRC и z1 = 17 при Н > 52 HRC.
Число зубьев неподвижного центрального колеса 3 определяют по заданному передаточному числу u:
z3 = z1(u – 1).
Число зубьев z2 сателлита 2 вычисляют из условия соосности, в соответствии которым межосевые расстояния aw зубчатых пар с внешним и внутренним зацеплением должны быть равны. Из рис. 1 для немодифицированной прямозубой передачи:
aw = 0,5(d1 + d2) = 0,5(d3 – d2), (1)
где d = mz - делительные диаметры колес.
Так как модули зацеплений планетарной передачи одинаковые, то формула (1) принимает вид:
z2 = 0,5(z3 – z1).
Полученные числа зубьев z1, z2, и z3 проверяют по условиям сборки и соседства.
Условие сборки требует, чтобы во всех зацеплениях центральных колес с сателлитами имело место совпадение зубьев со впадинами, в противном случае собрать передачу будет невозможно. Установлено, что при симметричном расположении сателлитов условие сборки удовлетворяется, когда сумма зубьев центральных колес (z1 + z3) кратна числу сателлитов с = 2…6 (обычно с = 3), т. е. должно соблюдаться условие:
(z1 + z3)/c = целое число.
Условие соседства требует, чтобы сателлиты не задевали зубьями друг друга. Для этого необходимо, чтобы сумма радиусов вершин зубьев соседних сателлитов, равная da2 = m(z2 + 2) , была меньше расстояния l между их осями (рис. 1), т. е.:
da2 < l = 2aw sin (180˚/c), (2)
где aw = 0,5m(z1 + z2) – межосевое расстояние.
Из формулы (2) следует, что условие соседства удовлетворяется, когда
z2 + 2 (z1 + z2) sin (180˚/c). (3)
***
Расчет на прочность планетарных передач
Расчет на прочность зубчатых передач планетарного типа ведут по методике, применяемой для обычных зубчатых передач. Основными критериями работоспособности для большинства планетарных передач (как и для всех зубчатых передач), является усталостная контактная прочность рабочих поверхностей зубьев и прочность зубьев при изгибе. При этом под контактной прочностью понимают способность контактирующих поверхностей зубьев обеспечить требуемую безопасность против прогрессирующего усталостного выкрашивания, а прочностью при изгибе – способность зубьев обеспечить требуемую безопасность против усталостного излома зуба.
Расчет выполняют для каждого зацепления. Например, в передаче, изображенной на рис. 1, необходимо рассчитать внешнее зацепление колес 1 и 2 и внутреннее – колес 2 и 3. Так как модули и силы в этих зацеплениях одинаковы, а внутреннее зацепление по своим свойствам прочнее внешнего, то при одинаковых материалах колес достаточно рассчитать только внешнее зацепление.
Расчет начинают с подбора чисел зубьев колес, как было показано выше.
При определении допускаемых напряжений коэффициенты долговечности находят по эквивалентных числам циклов нагружения. При этом число циклов перемены напряжений зубьев за весь срок службы вычисляют при вращении колес только относительно друг друга.
При определении допускаемых напряжений изгиба для зубьев сателлита вводят коэффициент YA, учитывающий двустороннее приложение нагрузки (симметричный цикл нагружения).
Межосевое расстояние планетарной прямозубой передачи для пары колес внешнего зацепления (центральной шестерни с сателлитом) определяют по формуле:
aw = 450(u’ + 1)× 3√{(КНТ1Кc)/(ψbau'[σ]Н2с)},
где u' = z2/z1 – передаточное число рассчитываемой пары колес;Кc = 1,05…1,15 – коэффициент неравномерности распределения нагрузки между сателлитами; Т1 – вращающий момент на валу центральной шестерни, Нм; с – число сателлитов; ψba - коэффициент ширины венца колеса: ψba = 0,4 для Н ≤ 350 НВ; ψba = 0,315 при 350 НВ < Н ≤ 50 HRC, ψba = 0,25 для Н > 50 HRC.
Ширина b3 центрального колеса 3 определяется по формуле b3 = ψbaaw. Ширину b2 венца сателлита принимают на 2…4 мм больше значения b3; ширина центральной шестерни b1 = 1,1b2.
Модуль зацепления определяют по формуле:
m = 2aw/(z2 + z1).
Получнный расчетом модуль округляют до ближайшего стандартного значения, а затем уточняют межосевое расстояние:
aw = m(z2 + z1)/2.
Окружную силу Ft в зацеплении вычисляют по формуле:
Ft = 2×103КcТ1/сd1.
Радиальную силу Fr определяют по формуле:
Fr = Ft tg αw,
где αw = 20˚ – угол зацепления.
***
Волновые передачи
k-a-t.ru
Строим планетарную КПП, часть 1: планетарные ряды: thunder_games
В предыдущих статьях о трансмиссиях я касался только двухвальных, трёхвальных и безвальных коробок передач, а планетарные обходил стороной. На сей раз я решил подробно описать работу планетарных коробкок передач фирмы Pulsgetriebe для Тигра и прототипа Леопарда. Однако я не мог уместить в один пост и объяснение принципов работы планетарных редуторов, и рассмотрение простой планетарной коробки передач, и, наконец, описание реальных КПП Pulsgetriebe. Поэтому я написал три поста: в первых двух объясняется, как работают планетарные редукторы и коробки передач, а в третьем дано описание коробок передач PP33 и PP45.
Если вы понимаете, как работают планетарные КПП, сразу переходите к третьему посту. Если нет, то прочтите этот пост и его вторую часть. В них я исхожу из того, что читатель знает, как работают двухвальные или трёхвальные коробки передач, но ничего не понимает в планетарных передачах.
ПРДПВ:
Устройство планетарной передачиДля того, чтобы изучить, как работает простая коробка передач, нужно сперва понять, как работает простейший редуктор из пары шестерён, а затем из таких пар собрать коробку передач. Мы поступим аналогично: сперва разберёмся с планетарными редукторами, а затем посмотрим, как их можно применить. Скажу сразу: люди придумали очень много планетарных механизмов и очень много схем планетарных коробок передач, всё их многообразие мы, конечно, охватить не сможем.
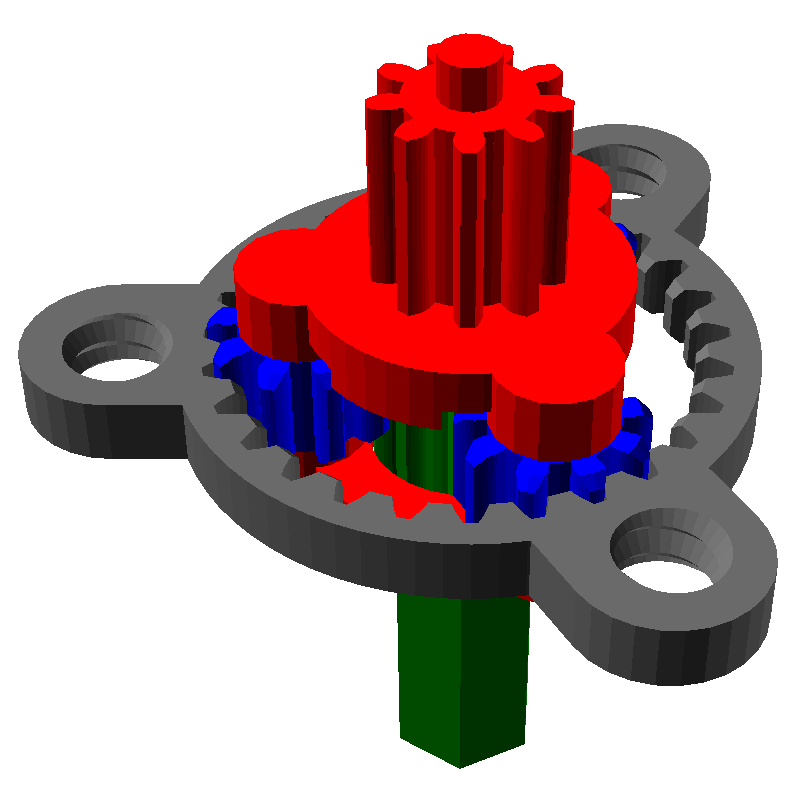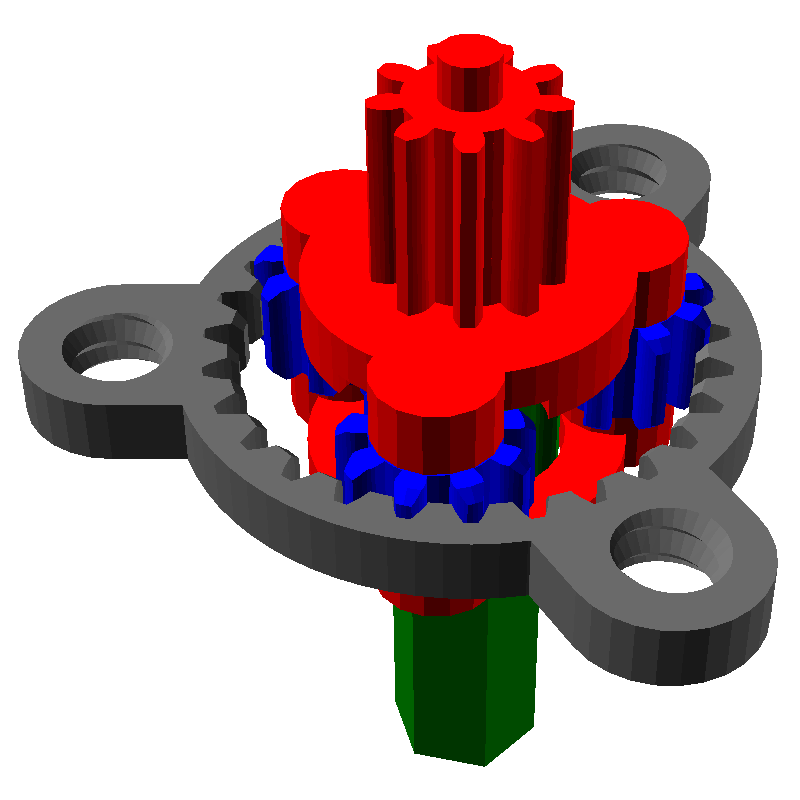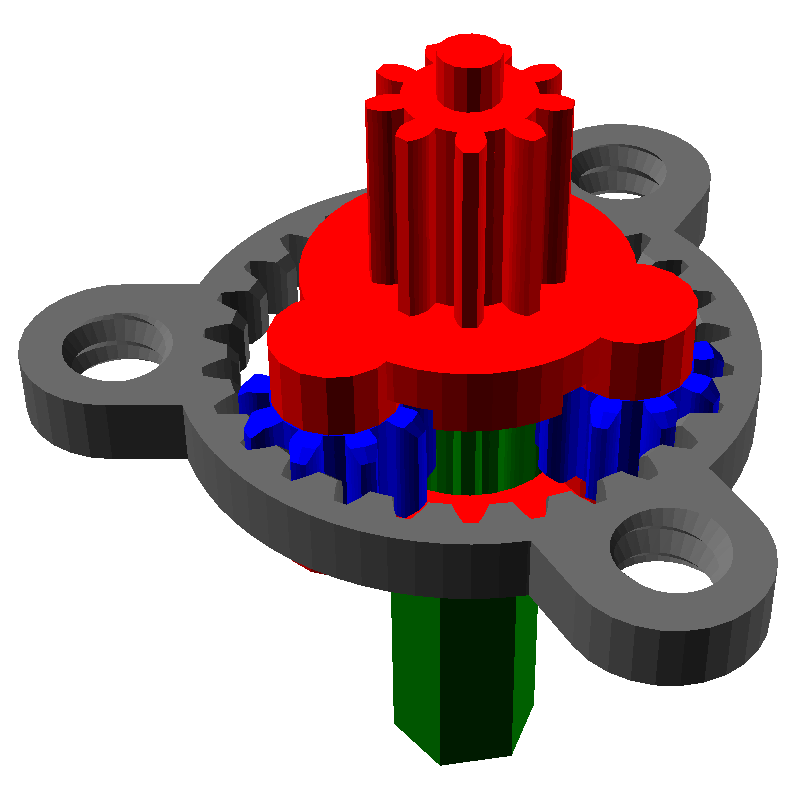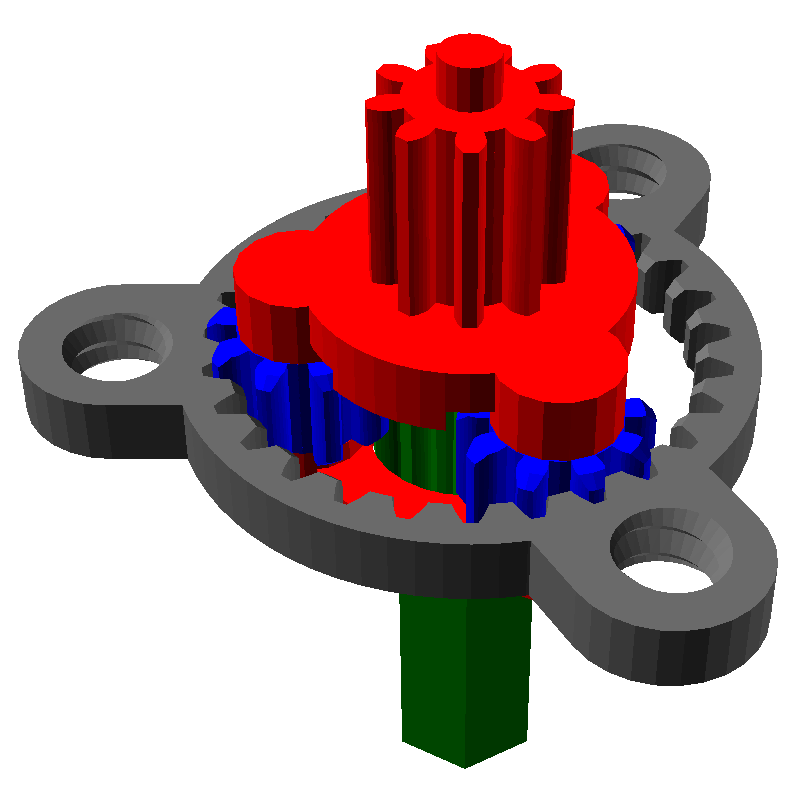
Один из самых распространённых планетарных механизмов выглядит следующим образом:
Он состоит из трёх частей:
- Солнечная шестерня, выделена красным
- Эпициклическая шестерня (или просто эпицикл) с внутренними зубьями, выделен зелёным
- Шестерни-Сателлиты, связывающие солнечную шестерню с эпициклом
У данной передачи есть три части: солнечная шестерня, эпицикл и водило. Если мы заблокируем одну из частей и начнём вращать другую, то начнёт вращаться третья. Её скорость вращения будет зависеть от чисел зубьев шестерён. Например, заблокируем серый эпицикл и начнём вращать красное водило, при этом будет вращаться и зелёный ведомый вал от солнечной шестерни:
Рассмотрим все три случая. Для того, чтобы анимация не мешала читать, я не буду вставлять сами картинки, но дам ссылки на них:
Планетарные редукторыДля того, чтобы использовать планетарную передачу как редуктор, нужно связать один элемент с ведущим валом, второй с ведомым, а третий заблокировать.
Вот схема редуктора с заблокированным эпициклом: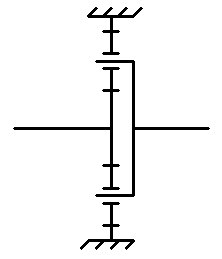
С заблокированной солнечной шестернёй: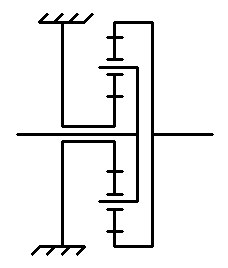
С заблокированным водилом: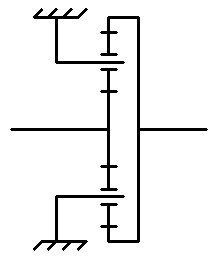
Планетарные редукторы имеют целый ряд достоинств перед обычными. Во-первых, мощность передаётся через несколько шестерён, как следствие, при прочих равных меньше нагрузка на зубья, выше надёжность и срок службы. Во-вторых, ведущий и ведомый валы соосны, часто это очень удобно с точки зрения компоновки. В-третьих, планетарная передача более компактна, чем простой редуктор с тем же передаточным числом: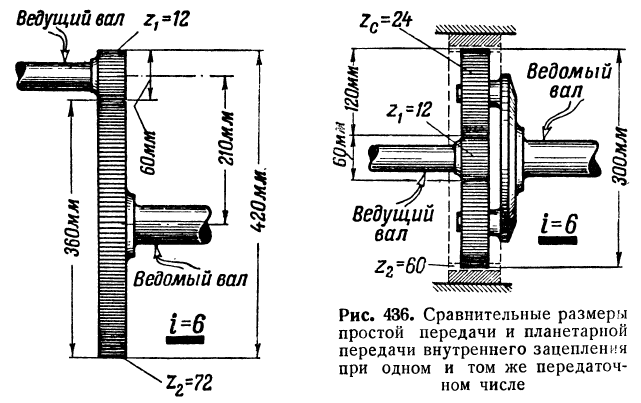
Планетарный однопоточный механизм поворотаПланетарную передачу можно использовать не только как редуктор, но и в механизме поворота. На среднем танке Шерман, например, механизм поворота двойной дифференциал, а это тоже планетарный механизм. Но мы рассмотрим механизм поворота не дифференциального, а независимого типа.
На схемах выше мы жёстко блокировали один из элементов планетарного механизма, поэтому он всегда работал как редуктор, передавая мощность. Давайте уберём эту блокировку и добавим ленточный тормоз: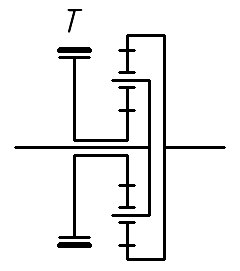
Представим, что двигатель связан с эпициклом, а водило с ведущими колёсами танка. Когда тормоз Т выключен происходит следующее. Двигатель вращает эпицикл, сателлиты и солнечную шестерню. Водило связано с ведущими колёсами, для того, чтобы оно вращалось нужно сдвинуть танк с места. Разумеется, намного проще вращать солнечную шестерню вхолостую, поэтому именно водило будет неподвижным. Для того, чтобы танк начал движение, нужно затянуть тормоз Т. Солнечная шестерня будет заблокирована и мощность пойдёт через водило к ведущим колёсам.
Осталось добавить остановочные тормоза и мы получим механизм поворота:
Тормоза Т2 и Т4 - остановочные, они тормозят ведущие колёса танка. Тормоза Т1 и Т3 называются опорными, они нужны для того, чтобы блокировать солнечные шестерни.
Для того, чтобы начать движение по прямой нам нужно выключить остановочные тормоза и затянуть опорные. Для поворота влево выключаем опорный тормоз Т1, а потом затягиваем остановочный тормоз Т2. Он тормозит левую гусеницу, мощность двигателя к ней не идёт. Для поворота вправо, соответственно, нужно выключить тормоз Т3 и занянуть Т4.
Планетарный механизм с внешним зацеплениемВыше мы рассмотрели планетарные механизмы с внутренним зацеплением, поскольку у их эпициклов внутренние зубья. Существуют аналогичные механизмы внешнего зацепления. В них используются эпициклы с внешними зубьями.
Всё познаётся в сравнении. Слева уже знакомый нам планетарный редуктор с заблокированным водилом и эпициклом внутреннего зацепления, а справа его аналог, тоже с заблокированным водилом, но с внешним зацеплением: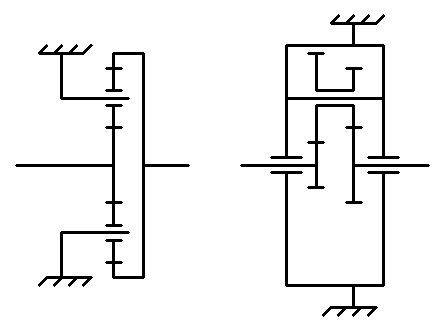
Давайте разберёмся, из каких частей он состоит и как работает.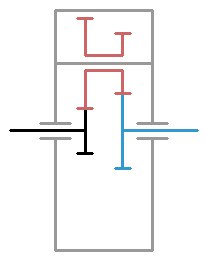
Чёрным цветом выделена солнечная шестерня, синим - эпицикл, красным - сдвоенный сателлит, а серым помечено водило.
Если заблокировать водило и начать вращать солнечную шестерню, то она станет вращать сателлит и через него эпицикл. Если заблокировать эпицикл и вращать солнечную шестерню, то будет вращаться водило. Одним словом, принцип работы точно такой же, просто другое исполнение.
На этом пока остановимся. В следующем посте на основе этих механизмов мы сделаем простейшие двухскоростные коробки передач и реверс, а затем соберём из них планетарную коробку передач и проанализируем её работу.
Читать дальше
thunder-games.livejournal.com
Планетарные ряды - Большая Энциклопедия Нефти и Газа, статья, страница 1
Планетарные ряды
Cтраница 1
Планетарные ряды и фрикционные элементы каждой коробки передач смонтированы в отдельном корпусе, который присоединяется специальным фланцем к раме трактора. [1]
Компонуя планетарные ряды, получают сложные, многоскоростные коробки передач. [2]
Так как в данной схеме планетарные ряды находятся в одном картере с тормозами, последние обычно работают в масле. [3]
Иногда различные лопаточные венцы соединяют через планетарные ряды, чем расширяется рабочая область гидротрансформатора. [4]
В схеме, изображенной на рис. 12.7, б, планетарные ряды выполнены с шестернями внешнего зацепления. [6]
На схеме рис. 14.1, д показан одноступенчатый планетарный механизм поворота, в котором рабочие планетарные ряды А выполнены по схеме, изображенной на рис. 14.1, в. Планетарные ряды Б служат только для уменьшения тормозного момента на тормозах 7, что облегчает управление механизмом поворота. Коронные шестерни 12 этого ряда неподвижно закреплены в корпусе 4 заднего моста, а его сателлиты 11 установлены на пальцах водил 13, являющихся одновременно приводом коронных шестерен 14 рабочего ряда А. При затянутых тормозах 7 солнечные шестерни 10 блокируют ряд Б, удерживая тем самым от проворачивания коронные шестерни 14 рабочего ряда А. Ленточные тормоза 7 и Т2 - остановочный - работают обычно в масле. [7]
На схеме рис. 14.1, д показан одноступенчатый планетарный механизм поворота, в котором рабочие планетарные ряды А выполнены по схеме, изображенной на рис. 14.1, в. Планетарные ряды Б служат только для уменьшения тормозного момента на тормозах 7, что облегчает управление механизмом поворота. Коронные шестерни 12 этого ряда неподвижно закреплены в корпусе 4 заднего моста, а его сателлиты 11 установлены на пальцах водил 13, являющихся одновременно приводом коронных шестерен 14 рабочего ряда А. При затянутых тормозах 7 солнечные шестерни 10 блокируют ряд Б, удерживая тем самым от проворачивания коронные шестерни 14 рабочего ряда А. Ленточные тормоза 7 и Т2 - остановочный - работают обычно в масле. [8]
Две рассмотренные схемы ( неприведенная и приведенная) замкнутого планетарного редуктора с дифференциальным рядом позволяют отметить некоторые особенности построения этих схем. Если планетарные ряды ( кроме дифференциального), образующие замкнутый редуктор, представляются в схеме полными динамическими графами, то таким же графом представляется и дифференциальный ряд. Если хотя бы один из указанных планетарных рядов представляется в динамической схеме редуцированным графом, то дифференциальный ряд представляется полным дифференциальным динамическим графом. [9]
Конструкция планетарной коробки передач аналогична рассмотренной выше и состоит из четырех планетарных рядов, управляемых с помощью четырех дисковых тормозов. Все планетарные ряды выполнены с одинарными сателлитами. [10]
Оценка влияния упругих свойств соединений, связывающих центральные колеса планетарных рядов многорядного редуктора с опорным звеном, производится так же, как для одно - и двухступенчатых планетарных передач. При определении схемных передаточных отношений учитываются кинематические свойства лишь тех планетарных рядов многорядного редуктора, которые представляются в общей динамической схеме редуцированными графами. Планетарные ряды, характеризуемые полными динамическими графами, рассматриваются как механизмы без редукции. [11]
В отечественных колесных тракторах наибольшее распространение имеют конечные передачи с неподвижными осями и цилиндрическими прямозубыми эвольвентными шестернями с внешним зацеплением. Цилиндрические шестерни с внутренним зацеплением, позволяющие иметь большое передаточное число этих передач, вследствие сложности их центрирования пока распространения в отечественных тракторах не получили. Конические шестерни иногда применяются в конечных передачах тракторов с ведущими управляемыми колесами. Планетарные ряды, конструктивно компактные, в настоящее время применяются только в конечных передачах особо мощного колесного трактора К-700, что связано с требованиями соблюдения дорожных габаритов ведущих мостов этого трактора. В колесных тракторах с силой тяги до 1 4 т наибольшее место занимают одноступенчатые однопарные конечные передачи. [12]
Страницы: 1
www.ngpedia.ru
Планетарный ряд
ПЛАНЕТАРНЫЙ РЯД
Ведущий подвижный конус (шкив) с помощью подшипников (шести шариков) опирается на ведущий вал вариатора и соединяется с ним с помощью планетарного механизма. Планетарный механизм используется для организации передачи заднего хода.
Планетарный механизм состоит из следующих элементов:
- солнечной шестерни,
- сателлитов,
- водила,
- эпицикла.
На снимке: планетарный механизм.
На снимке: планетарный механизм и муфта переднего хода (фрикционы).
На снимке: муфта заднего хода (фрикционы).
1 - большое стопорное кольцо для снятия фрикционов заднего хода
На снимке: поршень заднего хода, возвратная пружина поршня после снятия фрикционов.
1 - поршень заднего хода,
2 - возвратная пружина поршня заднего хода.
Ниже скриншоты, по которым можно найти запчасть здесь.
Ниже запчасти можно посмотреть здесь.
www.avtoakpp-cvt.ru
Планетарный ряд - Большая Энциклопедия Нефти и Газа, статья, страница 2
Планетарный ряд
Cтраница 2
Рассмотрим установившиеся колебания подвески планетарного ряда под действием сил взаимодействия эпицикла с сателлитами. [16]
При указанном динамическом представлении планетарного ряда с абсолютно жестко остановленным звеном q для сохранения цепной структуры общей динамической схемы необходимо осуществить приведение координат и упруго-инерционных параметров этой схемы. [17]
Рассмотрим установившиеся колебания подвески планетарного ряда под действием сил взаимодействия эпицикла с сателлитами. [18]
Она состоит из двух планетарных рядов. Каждый ряд имеет два управляющих элемента с электромагнитным приводом, что дает четыре передачи. Для получения заднего хода служит механизм реверса с ручным приводом управления. [19]
Основу любой планетарной передачи составляет планетарный ряд. На рис. 35.7, а приведена одна из возможных схем планетарного ряда со смешанным зацеплением шестерен. Зубья сателлита находятся в постоянном зацеплении с центральной а и коронной с шестернями. [21]
Под нагрузкой работает только второй планетарный ряд. Солнечная шестерня 8 является ведущим, а водило 9 - ведомым элементом. Оно вращается в том же направлении, что и солнечная шестерня, но с уменьшенной скоростью. [23]
Первая цифра индекса обозначает элемент планетарного ряда, вторая - порядковый номер планетарного ряда. [24]
Ведущее колесо, являющееся водилом планетарного ряда, вращается от сателлитов, установленных на роликоподшипниках. Наружные обоймы этих подшипников имеют внутренние бурты, фиксирующие сателлиты в осевом направлении. Оси сателлитов запрессованы в водило, а внутренние обоймы роликоподшипников сателлитов закреплены гайкой. Неподвижным элементом планетарного ряда является коронная шестерня, которая жестко соединена с корпусом машины при помощи шлицев. [25]
Это уравнение является общим для планетарного ряда, выполненного по любой схеме со смешанным зацеплением. [26]
Простой многорядный планетарный редуктор помимо планетарных рядов может содержать двухступенчатые планетариые передачи. Это не накладывает никаких особенностей на процесс построения динамической схемы редуктора, так как полные динамические графы двухступенчатой планетарной передачи и планетарного ряда структурно идентичны. [27]
Эта коробка состоит из двух планетарных рядов. [28]
В произвольном масштабе строим схему планетарного ряда, проводим ось, являющуюся продолжением центральной оси, восстанавливаем перпендикуляр к оси и сносим на него полюса зацепления. Соединяем конец вектора и с полюсом заторможенной шестерни прямой линией. От ведомого полюса откладываем вектор скорости, равный расстоянию от полюса до проведенной прямой. Из точки пересечения перпендикуляра с центральной осью проводим лучи к концам векторов скоростей. [29]
Результаты, полученные выше при анализе планетарного ряда, будут справедливы и для двухступенчатой планетарной передачи. При учете упругих свойств подшипниковых опор сателлитов реальной двухступенчатой планетарной передаче соответствует схематизированная условная двухступенчатая передача с безынерционным водилом. Связь его с конструктивным водилом осуществляется посредством соединения, эквивалентного по своей упругой характеристике опорам сателлитов. [30]
Страницы: 1 2 3 4
www.ngpedia.ru
Планетраные передачи
Планетарными механизмаминазываются зубчатые механизмы, у которых есть зубчатые колеса , оси которых подвижны. Это более сложные механизмы, чем рассмотренные ранее последовательные и ступенчатые ряды. В этих механизмах имеются зубчатые колеса, оси вращения которых перемещаются в прострнстве.
Рассмотрим схему одного из таких механизмов и его работу.
Название звеньев:
Звено ось которого подвижна в планетарном механизме называется сателлитом
с- сателлит
В планетарном механизме есть центральные звенья, оси которых совпадают с осью редуктора.
К ним относятся
а - солнечное колеса
в- эпициклическое колесо , коронное, венцовое колеса ( эпицикл, коронка, венец)
Н- водило .На водиле расположены оси вращения сателлитов
У планетарного механизма 4 звена. n=4
Число пар 5 го класса 4 . р5=4
Число пар 4 го класса 2. р4=2
Степень подвижности механизма по формуле Чебышева П.Л. W=3n-2p5-p4=3*4-2*4-2=2
То есть степень подвижности планетарного механизма с четырьмя подвижными звеньями равна двум.
Такой планетарный механизм называется дифференциальный. Он работает от двух двигателей , содержит два механизма первого класса.
Если одно из звеньев затормозить, связать со стойкой, то получим следующее соотношение звеньев и кинематических пар.
Число подвижных звеньев n=4
Число пар 5 го класса 3 . р5=3
Число пар 4 го класса 2. р4=2
Степень подвижности механизма по формуле Чебышева П.Л. W=3n-2p5-p4=3*3-2*3-2=1
То есть степень подвижности планетарного механизма с тремя подвижными звеньями равна 1.
Планетарный механизм с одной степенью подвижности называется планетарной передачей. Планетарные передачи имеют широкое применение в качестве силовых и кинематических передач. Они конкуренты многоступенчатых передач с неподвижными осями
Еще одной областью применения планетарных механизмов являются так называемые замкнутые планетарные передачи. В этих механизмах составной частью используется планетарный ряд у которого все 4 звена подвижны. Но , движение двух звеньев кинематически связаны друг с другом, наложено условие связи. В результате получим, что общий, более сложный механизм, так называемая замкнутая планетарная передача, имеет степень подвижности единица.W=1.
Планетарные механизмы имеют широкие области применения.
При этом достигаются:
малые габариты и вес в многосателлитных передачах
получение в одной ступени больших передаточных отношений, используется в не силовых приборных
передачах.
Сложение движений от двух двигателей с помощью дифференциальных механизмов
Многоступенчатые планетарные коробки скоростей, управляемые поочередным торможением звеньев
Лёгкое управление и регулирование скорости с помощью замкнутых планетарных передач.
Основные достоинства планетарных механизмов это малые габариты и вес при высокой несущей способности и КПД.
Это происходит из за
Распределения нагрузки между многими сателлитами, число сателлитов бывает от 2 до 20.
Большим передаточным отношение в одной ступени
Широкое применение в передаче внутренних зацеплений, обладающий высоким КПД.
Ограничимся рассмотрением планетарных передач и несколькими примерами замкнутых планетарных передач.
Построим картину скоростей планетарной передачи при заторможенном эпицикле. В этом варианте планетарный редуктор часто используется в силовых передачах.
H
H
a
a
b
b
В
В
c
nc
m
n
t
c
D
D
H
c
H
H
А
А
a
na
nH
c
a
c
a
На входе солнце а, на выходе водило Н.
Общая последовательность построения картины скоростей.
Сначала строим треугольник скоростей для входа, затем длясателлитаили блока сателлитов и последним длявыхода. Вот последовательность :вход , сателлиты, выход.
Когда строим картину скоростей для сателлита всегда ищем две точки: общую со стойкой, скорость которой равна нулю и общую с входом.
В нашем случае входным звеном является солнце, проводим линию , относящуюся к солнце под любым углом. Далее строим сателлит. Точка А будет общая точка сателлита с нулем, со стойкой, нулевым звеном. Скорость этой точки равна нулю, сносим ее на вертикальную ось. Точка В будет общая у сателлита со входом. Сносим ее на линию солнца. У сателлита известны две точки , через них проводим линию, являющуюся картиной скоростей для сателлита, это вторая линия. Наконец последняя линия для выходного звена, то есть для водила. Выходное звено всегда центральное, поэтому скорость его на оси равна нулю. Вторая точка с известной уже скоростью это точка на водиле общая с сателлитом . Это точка D. Сносим ее на линию сателлита. В результате построили три линии, которые образуют картину скоростей для планетарного ряда..
По картине скоростей расставим направление вращение звеньев. Вход и выход, солнце и водило вращаются в одну сторону. Сателлиты в другую, так как наклон эпюры скоростей сателлитов будет другой чем у солнца и водила. Это можно показать с помощью векторов оборотов na,nH ,nc, а также с помощью круглых стрелок угловых скоростейc, H, a
С помощью картины скоростей, если по всем осям выдержан масштаб, можно определить любые передаточные отношения. Например, передаточное отношение от солнца к водилу при заторможенном эпицикле. Отрезки mtиmnможно взять на отрезке прямой, проведенной на любом радиусе.
КИНЕМАТИКА ПЛАНЕТАРНЫХ ПЕРЕДАЧ.
Вывод общего уравнения кинематики планетаных передач.
Покажем универсальный способ определения различных передаточных отношений в планетарной передаче с помощью всего лишь одного уравнения- общего уравнения кинематики планетарной передачи. Для вывода этого уравнения воспользуемся методом инверсии или методом остановленного водила , методом Виллиса.
В планетарной передаче конструктора могут интересовать различные передаточные отношения. Напрмер при заторможенном эпицикле uaHb, ucHb , uHab,
При заторможенном солнечном колесе ubHa, ucHa , uHba и другие.
Самые простые передаточные отношения с точки зрения простоты их получения через числа зубьев, являются передаточные отношения при заторможенном водиле Н. При заторможенном водиле любой планетарный механизм превращается в паразитный или ступенчатый ряд. Как записать такие передаточные отношения через числа зубьев мы уже знаем. Например для нашего планетарного ряда
Оказывается ,что все другие передаточные отношения легко выражаются через эти, для этого выведем основное уравнение кинематики.
Для этого рассмотрим два движения. Первое основное движение . когда заторможенным является например эпицикл. Второе рассматриваемое движение это обращенное движение, когда всему механизму сообщается движение с угловой скоростью равной ωH но в противоположную сторону . При этом водило окажется неподвижным, при этом угловые скорости всех звеньев изменяться на величину -ωH.
32
32
Основное движение Обращенное движение
Угловые скорости в основном и обращенном движении
Основное движение Обращенное движение
Это два равноправных движения, в каждом из них можем записывать передаточные отношения.
Запишем в обращенном движении передаточное отношение от солнца к эпициклу и немного преобразуем его
Итак получаем общее уравнение кинематики
Либо в общем виде
Это уравнение необходимо запомнить Оно читается как : передаточное отношение от какого-то звена m к водилу H при остановленном звене n равно единице минус передаточное отношение от m к n при остановленном H , при это во втором передаточном отношении надо просто поменять индексы местами по диагонали.
Рассмотрим различные примеры использования общего уравнения кинематики при определении передаточных отношений различных схем планетарных передач.
РЯД ДЖЕМСА.
Этот ряд называют еще простой планетарный ряд, эпициклический ряд, ряд авН
Набольшее распространение этот ряд имеет в качестве силовой передачи, редуктора, при заторможенном эпицикле.
Строим картину скоростей. Вход –солнце, под любым углом. Сателлит- две точки: с нулём и со входом. Выход – водило : ноль на оси и общая точка с сателлитом. Расставляем в соответствии с картиной и наклом эпюр скоростей вектора оборотов звеньев и круглые стрелки угловых скоростей .
Найдем различные передаточные отношения аналитическим методом с помощью общего уравнения кинематики
От солнца к водилу, при этом меняем индексы по диагонали и для написания передаточного отношения от солнца к эпициклу при заторможенном водиле смотрим на схему. Имеем паразитный ряд у которого одно внешнее зацепление, поэтому знак минус
От сателлита к водилу
Рассмотрим пример za=12 ,zb=60,zc=24 , число оборотов солнца , звена на входе равно
na= 1000 об\.мин
Передаточные отношения нужны, чтобы определять частоту вращения звеньев и направление вращения
u aHb=na/nH=1-zb/za=1+60/12=6 откудаnH=na/uaHb=1000/6=166,7 об\мин
Обороты водила в 6 раз медленнее оборотов солнца и направлены в ту же строну.
Найдем обороты сателлита из передаточного отношения ucHb
ucHb=nc/nH=1-zb/zc=1- 60/24=-1,5 откудаnc=nH*ucHb=166,7*1,5=250,05 об\мин
Здесь знак в оборотах, при подстановке передаточного отношения, опущен ; мы ищем модуль оборотов.
Знание всех оборотов позволяет найти важное для конструктора число : относительные обороты сателлита относительно водила. По относительным оборотам рассчитываются подшипники качения, на которыxсидит сателлит на оси водила.
__ __ __
nс(Н)= nc- nH
nH
nc
nc(H)
nс(Н)=nc+nH=250,05+166,7=416,75 об\мин
На эти обороты и необходимо рассчитывать подшипники качения.
Общее замечание состоит в том, что если вектора абсолютных скоростей сателлитов и водила направлены в разные стороны , то при подсчете относительных оборотов модули векторов складываются , если в одну, то вычитаются. В
В нашем варианте в разные , поэтому складываются.
Часто отношение чисел зубьев zb/za равное |uabH| обозначают через к и называют характеристикой планетарного ряда.
Характеристика планетарного ряда
Передаточное отношение от солнца к водилу через характеристику планетарного ряда запишется как
Характеристика планетарного ряда характеризует габариты планетарной передачи. С ростом к, с ростом передаточного отношения, растет радиус эпицикла и габариты передачи. Отсюда ограничение на конструктивно целесообразное максимальное передаточное отношение равное 8 в таком ряду.
Минимальное передаточное отношение также ограничено , оно около 3. При уменьшении к сближаются значения радиусов rb и ra и не остается места сателлитам. Итак диапазон передаточных отношений и КПД равны.
uaНв= 2,7….8 при этом КПД= 0,98…0,97
Следующая схема это модифицированный рад ДЖЕМСА. В этой схеме сателлит заменен блоком сателлитов.
МОДИФИЦИРОВАННЫЙ РЯД ДЖЕМСА или эпициклический ряд с внешним и внутренним зацеплением.
0
a
H
m
n
t
c
Строим картину скоростей. Вход –солнце, под любым углом. Сателлит- две точки: с нулём и со входом. Выход – водило : ноль на оси и общая точка с сателлитом. Расставляем в соответствии с картиной и наклом эпюр скоростей вектора оборотов звеньев .
Найдем различные передаточные отношения аналитическим методом с помощью общего уравнения кинематики
От солнца к водилу, при этом меняем индексы по диагонали и для написания передаточного отношения от солнца к эпициклу при заторможенном водиле смотрим на схему. Имеем ступенчатый ряд у котрого одно внешнее зацепление и одно внутреннее, поэтому знак минус Движение передаем в ряду от а к с1 и от с2 к b.
От сателлита к водилу
За счет блока сателлитов расширяется диапазон допустимых передаточных отношений
uaHb= 2…15 КПД высок= 0,98…0,97
РЕДУКТРОР ДАВИДА С ДВУМЯ ВНУТРЕННИМИ ЗАЦЕПЛЕНИЯМИ
Строим картину скоростей. Вход –водило, под любым углом. Сателлит- две точки: с нулём и со входом. Выход – эптцикл : ноль на оси и общая точка с сателлитом. Расставляем в соответствии с картиной и наклоном эпюр скоростей вектора оборотов звеньев .
Найдем различные передаточные отношения аналитическим методом с помощью общего уравнения кинематики
В этой схеме, чтобы получить редуктор ведущим должно быть водило, ведомым эпицикл. В этом передаточном отношении неправильное расположение нижних индексов. Чтобы воспользоваться общим уравнением кинематики надо поменять нижние индексы. Для этого делим единицу на ub2Hb1. И дальше общее уравнение кинематики.
Передаточное отношение от сателлита к водиу.
В этой схеме диапазон допустимых передаточных отношений и КПД
uHb2b1= 30 … 1000 КПДη= 0,9 ….0,1
Эта схема используется, в основном, в качестве кинематических передач.
| u | 30 | 50 | 100 | 200 | 500 | 1000 |
| | 0,9 | 0,75 | 0,6 | 0,45 | 0,25 | 0,12 |
РЕДУКТОР ДАВИДА С ДВУМЯ ВНЕШНИМИ ЗАЦЕПЛЕНИЯМИ
Строим картину скоростей. Вход –водило, под любым углом. Сателлит- две точки: с нулём и со входом. Выход – солнечное колесо а2 : ноль на оси и общая точка с сателлитом. Расставляем в соответствии с картиной и наклоном эпюр скоростей вектора оборотов звеньев .
В этой схеме, чтобы получить редуктор, ведущим должно быть водило, ведомым солнце. В этом передаточном отношении неправильное расположение нижних индексов. Чтобы воспользоваться общим уравнением кинематики надо поменять нижние индексы. Для этого делим единицу на uа2Hа1. И дальше общее уравнение кинематики.
Передаточное отношение от сателлита к водиу.
В этой схеме диапазон допустимых передаточных отношений
uHа2а1= 2 … 300
КПД значительно ниже чем в предыдущей схеме, так как здесь два внешних зацепления.
Эта схема используется, в основном, в качестве кинематических передач.
ПЛАНЕТАРНАЯ ПЕРЕДАЧА СО СВОБОДНЫМ ВОДИЛОМ
Планетарная ступень со свободным водилом на самом деле представляет собой две последовательно соединенные ступени. Размеры звеньев таковы, что эти две ступени можно слить в одну и значительно уменьшить осевые габариты Свободное водило обозначает то что водило не является ни входным ни выходным звеном. Оно внутри, поддерживает сателлиты.
РАСШИФРОВКА СХЕМЫ И КАРТИНА СКОРОСТЕЙ
На этом рисунке показано как расшифровывается схема со свободным водилом. В первой ступени движение передается от входа , солнца к водилу. Во второй ступени об водила к выходу , которым в данной схеме является эпицикл b2. Сателлиты с1 и заторможенные эпициклы b1 одинаковы в обеих схемах . Если бы они были разными, это бы были чисто две планетарные ступени , соединённые последовательно. В нашем же случае , когда они одинаковы мы можем эти две ступени соединить в одну , при этом водило становится внутренним звеном , как бы свободным, не являющимся ни входным ни выходным.
Передаточное отношение в схеме со свободным водилом записывается также как и расшифровка то есть от входа к водилу и от водила к выходу при одном и том же заторможенном звене
Выразим через числа зубьев., первая ступень планетарный ряд Джемса, вторая ступень редуктор Давида с двумя внутренними зацеплениями.
Эта схема может использоваться и в качестве силовой, так как довольно высок КПД и в качестве кинематической, так как возможно большое передаточное отношение в одной ступени.
| u | 15 | 50 | 100 | 200 | 500 | 1500 |
| | 0,95 | 0,9 | 0,85 | 0,75 | 0,6 | 0,35 |
Приведем итоговую таблицу по планетарным передачам
Рассмотрим несколько примеров кинематического анализа зубчатых передач.
Последовательность анализа состоит из нескольких пунктов.
Проанализировать схему зубчатого механизма, определив сколько ступеней соединены последовательно от входа к выходу, как называются эти ступени с неподвижными звеньями и планетарные, от какого к какому звену в ступени передается движение.
Проверить правильность задания чисел зубьев через условие соосности в разных ступнях. Если необходимо, определить неизвестное число зубьев.
Вычертить кинематическую схему зубчатой передачи в масштабе и отметить на ней выходное и выходное звено с указанием направления вращения на входе. Модуль всех зубчатых колес принять равным m=1 мм.
Обозначить арабскими цифрами звенья передачи, при этом нужно отбросить, если они есть, параллельные ветви. Подсчитать степень подвижности механизма.
Построить картину скоростей для планетарных ступеней и определить и обозначить с помощью этой картины направление вращения звеньев планетарной ступени. Обозначить направление вращения и других звеньев.
По картине скоростей определить передаточное планетарной ступени, как отношение соответствующих отрезков.
Записать общее передаточное отношение зубчатого механизма, как произведение передаточного отношения ступеней.
Выразить через числа зубьев и, подставив значения чисел зубьев, численно подсчитать каждое передаточное отношение. Сравнить полученные значения передаточных отношения для планетарных ступеней со значениями, полученными с помощью картины скоростей.
Подсчитать численное значение общего передаточного отношения. Определить частоту вращения выходного звена.
Для планетарного механизма найти передаточное отношение от сателлита к водилу.
Зная частоту вращения входного звена, найти частоту вращения всех звеньев зубчатого механизма. Для сателлита, кроме того, найти относительные обороты сателлита относительно водила. При этом проверить по знаку передаточного правильность направления вращения, найденного по картине скоростей.
Пример 1
Решение
1. Кинематическая схема зубчатого механизма состоит из трех ступеней. Первая ступень - планетарная, простой планетарный ряд Джемса, движение передается от солнца z1к водилуH. Вторая ступень - цилиндрическая зубчатая передача внешнего зацепления, движение передается от шестерниz5кz6. Третья ступень - цилиндрическая передача внутреннего зацепления, движение передается от шестерниz7к зубчатому колесу с внутренними зубьямиz8. Зубчатое колесоz8является выходным звеном всего зубчатого механизма.
2. Можно записать два условия соосности: для планетарной ступени и для двух ступеней с неподвижными осями.
z4 - z2= z1 + z2 ; ? - 20 = 25 + 20 ;z4= 65 -
z5+ z6= z8- z7 ; 18 + 28 = ? - 14 ;z8=60
Число звеньев, число кинематических пар
n=5; P5=5; P4=4 W= 3n – 2*P5 - P4= 3*5 - 2*5 – 4 = 1
Передаточное отношение планетарного ряда с помощью картины скоростей
uz1Hz4=tgδ /tgβ = mt/mn=22/6=3,66
Общее передаточное отношение
u15=u13u34u45= uz1Hz4 u34u45=3,6*1,55*4,29=23,94
Передаточное отношение планетарной ступени
u13 =uz1Hz4=1- uz1z4H=1-(-z4/z1)=1+z4/z1=1+65/25=3,6
Передаточное отношение цилиндрической зубчатой передачи внешнего зацепления
u34=z6/z5=28/18=1,55
Передаточное отношение цилиндрической зубчатой передачи внутреннего зацепления
u45=z8/z7=60/14=4,29
Частота вращения выходного вала
n5=n1/ u15=1600/23,94=66,83 [об/мин]
n3= nH =n1/ u13=1600 / 3,6=444,44 [об/мин]
n4=n1/ (u13 u34)=1600/(3,6*1,55)=286,73 [об/мин]
Передаточное отношение от сателлита к водилу, воспользуемся общим уравнением кинематики
uСHz4=1- uСz4H=1-(z4/z2)=1-65/20=-2,25
Обороты сателлита определим как
nc/nH= uСHz4 nc= uСHz4 nH=2,25*444,44= 999,999 [об/мин]
Относительные обороты сателлита относительно водила
___ __ __
ncН= nc- nН ., в нашем случае угловые скорости сателлита и водила направлены в разные стороны.
Следовательно при определении модуля угловой скорости сателлита в относительном движении относительно водила модули абсолютных скоростей необходимо складывать.
ncН= nc+ nН = 999,999 + 444,444 = 1445 [об/мин]
Оценка работоспособности подшипников качения сателлитов будет производится именно по этим оборотам
Пример 2
studfiles.net
