Соленоид это: СОЛЕНОИД | это… Что такое СОЛЕНОИД?

СОЛЕНОИД | это… Что такое СОЛЕНОИД?

ТолкованиеПеревод

СОЛЕНОИД

СОЛЕНОИД

       

(от греч. solen — трубка и eidos — вид), свёрнутый в спираль изолированный проводник, по к-рому течёт электрич. ток. Обладает значит. индуктивностью и малым активным сопротивлением и ёмкостью. В ср. части внутр. полости С., длина к-рого значительно больше диаметра, магн. поле С. направлено параллельно его оси и однородно (рис.), причём его напряжённость пропорц. силе тока и (приближённо) числу витков.

Внеш. магн. поле С. подобно полю стержневого магнита. С. с железным сердечником во внутр. полости представляет собой электромагнит.

Физический энциклопедический словарь. — М.: Советская энциклопедия.
Главный редактор А. М. Прохоров.
1983.

СОЛЕНОИД

(от греч. solen — трубка и eidos — вид) — проволочнаяспираль с током, характеризуемая числом витков на единицу длины п, длиной l, диаметром d; толщина провода и шаг спирали (винтовой линии)малы по сравнению с d и l. Термин «С.» применяют и в болеешироком значении — так называют катушки с произвольным сечением (квадратныйС., прямоуг. С.), и не обязательно цилиндрические (тороидальный С.). Различаютдлинный С. (ld )и короткий (ld). В тех случаях, когда соотношение между d и l специальноне оговаривается, подразумевается длинный С. В теоретич. физике модельюС. служит система поверхностных токов j _П, текущих поцилиндрич. поверхности перпендикулярно к образующей (j _П= nI, где I -ток моделируемого С.).

С. изобретён в 1820 А. Ампером (A. Ampere) для усиления открытого X.Эрстедом (Н. Oersted) магн. действия тока и был применён Д. Араго (D. Arago)в опытах по намагничиванию стальных стержней. Магн. свойства С. были экспериментальноизучены Ампером в 1822 (тогда же им был введён и термин «С.»), была установленаэквивалентность С. постоянным природным магнитам той же конфигурации, чтоявилось подтверждением электродинамич. теории Ампера, объяснявшей магнетизмвзаимодействием скрытых в телах кольцевых молекулярных токов.

Энергия магн. поля С. с точностью до величины порядка d/l сосредоточенавнутри С. Вдали от концов С. внутр. поле близко к однородному с напряжённостью Н= пI в СИ (в гауссовой системе единиц H = 4pnI/с).Внеш. поле С. близко к полю двух магн. зарядов ±q^m, помещённыхна его концах [( — магн. постоянная)в СИ, вгауссовой системе единиц]. Силовые линии магн. поля С. приведены на рис.

С. используются в физике и технике для создания квазподнородных магн. Лит.: Калантаров П. Л., Цейтлин Л. А., Расчет индуктивностей,3 изд., Л., 1986; Фейнман Р., Лейтон Р., С э н д с М., Фейнмановские лекциипо физике, пер. с англ., [в.] 5, 2 изд., М., 1977. Г. В. Пермитин.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия.
Главный редактор А. М. Прохоров.
1988.

.

Поможем решить контрольную работу

Синонимы:

катушка

• СОВПАДЕНИЙ МЕТОД ИЗМЕРЕНИЙ
• СОЛЕНОИДАЛЬНОЕ ПОЛЕ

Полезное

Соленоид и электромагнит

В предыдущем параграфе мы изучали магнитные поля прямых проводников. Рассмотрим теперь проводник, свёрнутый в виде спирали, по которому идёт ток – соленоид (греч. «солен» – трубка). Расположим вдоль его оси лист картона и посыплем его железными опилками. На рисунке отчётливо видно, что опилки выстроились в виде замкнутых линий, наиболее часто расположенных внутри витков соленоида. Следовательно, магнитное поле внутри соленоида сильнее, чем вне его.

Намотаем теперь проволочную спираль на каркасе, располагая витки вплотную друг к другу – мы получим катушку (см. рисунки ниже). Включим ток и поднесём к катушке мелкие гвоздики – часть из них примагнитится. Если в неё вставить железный или стальной стержень – сердечник, то примагнитится заметно больше гвоздиков. Другими словами, происходит усиление магнитного поля.

Катушка из изолированной проволоки с железным сердечником внутри называется электромагнитом. При прочих равных условиях магнитное поле электромагнита всегда сильнее магнитного поля соленоида или катушки без сердечника.

Объясним усиление магнитного поля. Сначала ток намагничивает сердечник. Намагнитившись, он создаёт собственное поле, которое, складываясь с полем соленоида, образует новое, более сильное поле. Об этом мы судим по количеству притянувшихся гвоздиков.

Рассмотрим другие причины, влияющие на силу магнитного действия электромагнита. Вспомним, что для наблюдения силовых линий поля прямого проводника (см. § 10-а) мы использовали ток силой 5–10 А. При меньшей силе тока опилки будут плохо намагничиваться, и картинка получится нечёткой. Следовательно, магнитное поле электромагнита усиливается при увеличении силы тока в его проводнике.

Кроме того, при одной и той же силе тока поле электромагнита можно усилить, увеличив число витков проводника в его обмотке. Это объясняется тем, что магнитные поля, создаваемые каждым из витков, накладываются друг на друга и тем самым образуют новое, более сильное магнитное поле.

Познакомимся с ещё одним свойством электромагнита или соленоида – запасать электроэнергию.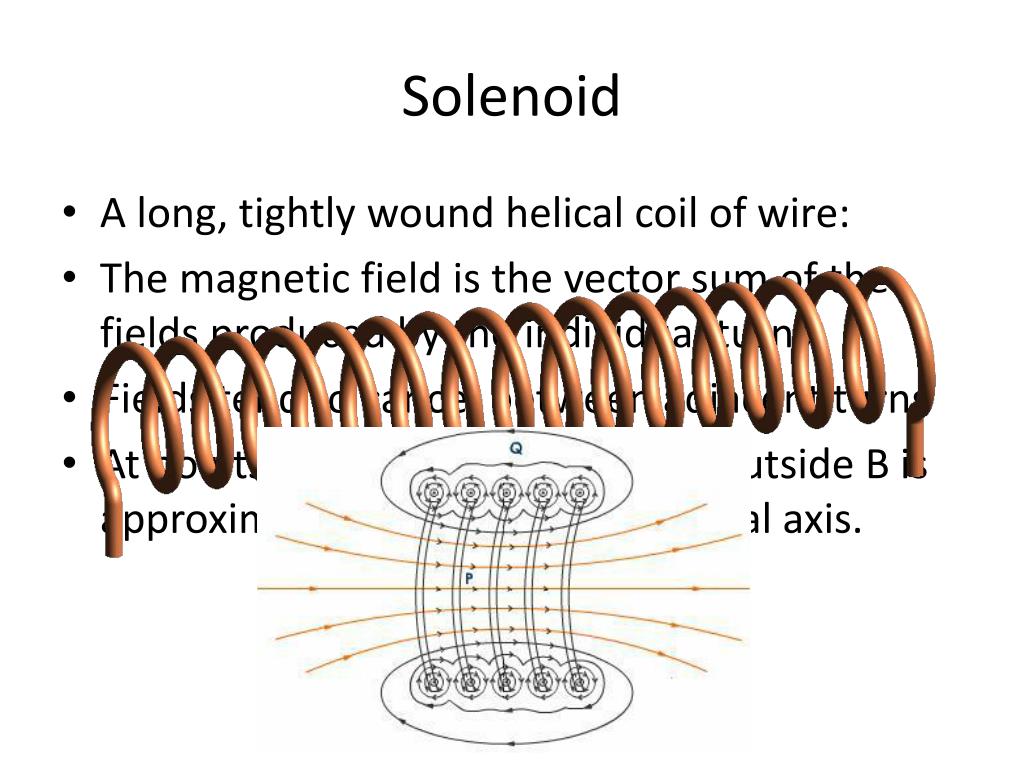 Проделаем опыт (см. схему). Две одинаковые лампы подключены параллельно к источнику тока. Верхняя лампа – через реостат, а нижняя – через электромагнит или соленоид. У них есть общее название – катушка индуктивности.

При замыкании выключателя лампа, соединённая с катушкой индуктивности, загорается позже, чем лампа, соединённая с реостатом (левый рисунок). Теперь разомкнём выключатель. В этот момент обе лампы не погаснут, а вспыхнут ещё ярче, правда, на очень короткое время (правый рисунок).

Более позднее загорание ближней к нам лампы объясняется так. При включении тока его энергия идёт не только на нагревание спирали лампы, но и на создание магнитного поля вокруг электромагнита. Однако по прошествии некоторого времени энергия тока будет целиком превращаться в теплоту, разогревая спираль лампочки настолько, что она начинает светиться.

При размыкании цепи ток в нижнем её проводе прекращается, и с этого момента реостат, катушка индуктивности и обе лампочки оказываются соединёнными друг с другом последовательно (мы это показали красным цветом на схеме). Поскольку лампочки кратковременно ярко вспыхнули, значит, в красной части цепи ненадолго возник источник тока. В его роли выступила катушка индуктивности. Магнитное поле вокруг неё стало исчезать, передавая свою энергию электронам в проводе, поэтому они приходят в движение. Это значит, что катушка становится источником тока.

Опубликовано в разделах: 8 класс, Электромагнитные явления

Объяснение урока: Магнитное поле, создаваемое током в соленоиде

В этом объяснении мы узнаем, как рассчитать магнитное поле, создаваемое
ток в соленоиде.

Вспомнить направление магнитного поля в петле провода с током. В центре петли магнитное поле имеет одно направление, как видно на
схема ниже. Оранжевая линия — направление магнитного поля, черная линия — направление магнитного поля.
петля.

Та же петля, вид спереди, с указанием направления магнитного поля
вне экрана, будет выглядеть как на диаграмме ниже.

Помните, что приведенные ниже символы используются для обозначения того, что направление выходит из или
в экран.

Напряженность магнитного поля в центре петли можно увеличить, поместив
больше петель в соответствии с ним. На диаграмме ниже показаны два набора петель с одинаковыми
тока и того же радиуса выстроились таким образом.

Набор петель справа имеет более сильное магнитное поле, потому что в нем больше
петли.

Вместо набора петель усиление магнитного поля в центре
может быть достигнуто с помощью одного провода с несколькими витками. На приведенной ниже диаграмме показано
такой провод, с видом сбоку и спереди.

Провод с таким набором витков называется соленоидом. Каждый ход
соленоид вносит свой вклад в силу магнитного поля в центре точно так же, как
дополнительная петля будет.

Напряженность и направление магнитного поля в самом центре соленоида
униформа. Он имеет одно направление и величину. Другие точки вокруг соленоида имеют
различные направления и величины магнитного поля.

Прежде чем рассматривать силовые линии магнитного поля соленоида, давайте рассмотрим
угол, с которого мы будем смотреть, используя один цикл. На приведенной ниже диаграмме показан
одиночный виток провода с током и его результирующее магнитное поле от двух
разные углы.

Вид сбоку этой петли показывает направление, в котором смотрит наблюдатель,
обозначенное глазом, чтобы получить вид сверху вниз. Вид сверху вниз по-прежнему
показывает направление тока, входящего и выходящего из экрана, но не
показать нижнюю часть петли.

Теперь давайте посмотрим на вид сверху вниз на одну петлю с ее магнитным
линии поля, выделенные серым цветом, на диаграмме ниже.

Когда силовые линии магнитного поля расположены близко друг к другу, это означает, что
более сильное магнитное поле. Мы видим, что в самом центре петли
силовые линии магнитного поля расположены очень близко друг к другу с одинаковым направлением, что означает
в этой точке у него сильное магнитное поле.

Вне контура силовые линии магнитного поля напоминают стержневой магнит,
как показано ниже.

Теперь посмотрим на соленоид с семью витками под этим углом. Диаграмма
ниже показано это с соответствующим магнитным полем.

Обратите внимание, что силовые линии магнитного поля постоянны и прямые в самом центре
эти провода поворачиваются, но становятся менее последовательными по направлению к концам соленоида.
ближе к этим концам, тем менее однородны силовые линии.

Теперь давайте рассмотрим теоретически очень длинный соленоид. Это так долго, что
мы можем относиться к нему так, как если бы у него не было концов. Это означало бы, что он имеет совершенно однородный
магнитное поле внутри витков во всех точках.

Если бы мы измерили напряженность магнитного поля в разных точках в пределах витков
этот теоретический соленоид, в каждом случае величина и направление магнитного
напряженность поля была бы одинаковой. На приведенной ниже диаграмме показан теоретический соленоид.
с тремя точками, обозначенными красными точками, которые имеют эквивалентное магнитное поле
сильные стороны и направления.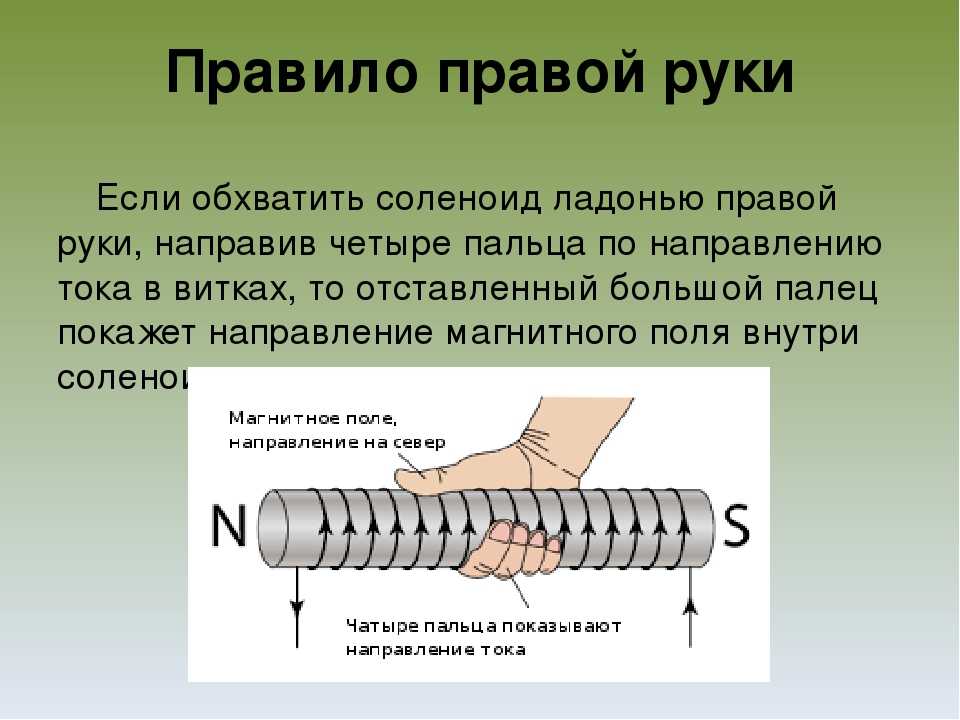

Напряженность магнитного поля внутри витков этого теоретического соленоида может быть
определяется с помощью уравнения.

Уравнение: напряженность магнитного поля в центре соленоида

Напряженность магнитного поля, 𝐵, внутри центра соленоида
находится с помощью уравнения
𝐵=𝜇𝑁𝐼𝐿,
где 𝐼 — ток соленоида,
𝑁 — количество витков соленоида,
𝐿 — длина соленоида, а
𝜇 — проницаемость свободного пространства,
4𝜋×10 Т⋅м/А.

Для реального соленоида с ограниченной длиной это уравнение по-прежнему полезно для
описывают напряженность магнитного поля точно в центре витков, так как это
там, где она однородна. На диаграмме ниже показаны точки с одинаковыми магнитными
напряженность и направление поля как на теоретическом, так и на реальном соленоиде.

Реальные соленоиды имеют достаточно постоянное направление магнитного поля внутри витков,
но не напряженность магнитного поля. Только центр имеет постоянное магнитное поле.
прочность.

Глядя на уравнение, мы видим, что длина соленоида имеет значение, когда
найти напряженность магнитного поля в центре. В частности, это магнитное
напряженность поля обратно пропорциональна длине. На схеме ниже показаны два
соленоиды с одинаковым током и числом витков, но с разным
длины.

Так как нижний соленоид в два раза длиннее, он будет иметь вдвое меньшую длину.
напряженность магнитного поля в его центре.

Давайте рассмотрим пример с использованием этого уравнения.

Пример 1: Напряженность магнитного поля в центре соленоида с витками и
Длина

Соленоид имеет длину
3,2 см
и состоит из 90 витков провода. По проводу течет постоянный ток
1,2 А. Рассчитайте напряженность магнитного поля в центре соленоида. Дайте свой ответ в
тесла
выражается в научной записи с точностью до одного десятичного знака. Используйте значение
4𝜋×10 Т⋅м/А
для 𝜇.

Ответ

Мы будем использовать уравнение
𝐵=𝜇𝑁𝐼𝐿
найти напряженность магнитного поля в центре этого соленоида.

Прежде чем мы сможем подставить значения, которые нам даны, мы должны убедиться, что
единицы все совпадают. Проницаемость свободного пространства использует
метры,
поэтому нам нужна длина
3,2 см в
метров.

Есть
100 сантиметров в
1 метр:
1100 мкм

Итак, чтобы преобразовать 3,2 см
в метры,
умножаем на соотношение
1100×3,2=0,032 мкм см

Таким образом, 3,2 см
составляет 0,032 м.

Теперь мы можем подставить значения в уравнение. Длина
0,032 м, ток
1,2 А, 90 витков,
а проницаемость свободного пространства
4𝜋×10 Т⋅м/А. Это дает нам
𝐵=𝜇𝑁𝐼𝐿𝐵=4𝜋×10⋅/(90)(1,2)0,032.TmAAm

Умножим в числителе. Это отменяет единицы
Ампер там,
давать
𝐵=1,36×10⋅0,032. Tмм

Итак, теперь, когда мы разделим эти два числа, единицы
метры отменить,
оставив только
тесла:
1,36×10⋅0,032=4,24×10,TmmT

Округлив до одного десятичного знака, напряженность магнитного поля в центре
соленоид
4,2×10 T.

Напряженность магнитного поля в центре уравнения соленоида можно использовать для нахождения
другие переменные в уравнении, если напряженность магнитного поля в центре
соленоид известен. Чтобы показать это, давайте посмотрим на основное уравнение и положим все
значения с точки зрения 𝐼. Начиная с уравнения
𝐵=𝜇𝑁𝐼𝐿,
мы можем умножить обе части на 𝐿:
𝐵×𝐿=𝜇𝑁𝐼𝐿×𝐿.

Это отменяет 𝐿 справа, оставляя позади
𝐵𝐿=𝜇𝑁𝐼.

Из этой формы мы можем разделить обе части на 𝜇
и 𝑁:
𝐵𝐿𝜇𝑁=𝜇𝑁𝐼𝜇𝑁.

Это отменяет 𝜇 и 𝑁 с правой стороны,
оставив только 𝐼:
𝐵𝐿𝜇𝑁=𝐼.

Давайте рассмотрим пример, используя эту форму уравнения.

Пример 2: Определение тока в соленоиде с витками и длиной

Соленоид состоит из 35 витков провода на длине
42 мм. Магнитное поле в центре соленоида измеряется как
4.9×10 Тл. Рассчитайте силу тока в проводе. Дайте ответ в амперах на
2 десятичных разряда. Используйте значение
4𝜋×10 Т⋅м/А
для 𝜇.

Ответ

Напомним, что уравнение
𝐵=𝜇𝑁𝐼𝐿
можно представить в виде, связывающем переменные с текущим:
𝐼=𝐵𝐿𝜇𝑁.

Перед тем, как мы непосредственно подставим полученные значения в эту форму
уравнение, мы должны убедиться, что единицы совпадают. Проницаемость свободного пространства
использует метры, поэтому нам нужна длина соленоида,
42 мм, чтобы также быть в
с точки зрения метров.

1‎ ‎000 миллиметров в
1 метр:
11000.mmm

Таким образом, умножая это отношение на
42 мм
даст нам значение в
метров:
11000×42=0,042. мммммм

Длина соленоида в метрах
составляет 0,042 м.

Теперь мы можем подставить значения в уравнение. Длина
0,042 м, магнитный
напряженность поля
4,9×10 Т,
витков 35, а проницаемость свободного пространства равна
4𝜋×10 Т⋅м/А. Это дает нам
𝐼=𝐵𝐿𝜇𝑁𝐼=4,9×10(0,042)(4𝜋×10⋅/)(35).TmTmA

Умножение на числитель дает единицы
Т⋅м:
𝐼=2,06×10⋅(4𝜋×10⋅/)(35).TmTmA

Количество витков в соленоиде безразмерно, поэтому умножение на
знаменатель не меняет единицы измерения:
𝐼=2,06×10⋅4,39×10⋅/.TmTmA

Разделение верхней части на нижнюю полностью аннулирует единицы
Т⋅м и уходи
за амперами на
вершина. Глядя только на единицы, деление на дробь такое же, как
умножение на обратное:
(⋅)(⋅/)=(⋅)×(⋅)=.TmTmATmATmA

Итак, деление чисел дает
2,06×10⋅4,39×10⋅/=0,468. TmTmAA

Округлив до двух знаков после запятой, ответ будет таким образом
0,47 A.

Уравнение можно записать и в терминах других переменных. Допустим, у нас есть соленоид с неизвестной длиной, но с другими известными
переменные. Начиная с основного уравнения
𝐵=𝜇𝑁𝐼𝐿,
мы можем получить длину одной стороны уравнения, умножив обе части на
𝐿:
𝐵×𝐿=𝜇𝑁𝐼𝐿×𝐿.

Отменяет 𝐿 справа, давая
𝐵𝐿=𝜇𝑁𝐼.

Затем мы делим обе части на 𝐵, чтобы получить
𝐵𝐿𝐵=𝜇𝑁𝐼𝐵,
который отменяет 𝐵 слева, оставляя только
𝐿:
𝐿=𝜇𝑁𝐼𝐵.

Давайте рассмотрим пример, использующий эту форму уравнения.

Пример 3: Длина соленоида

Соленоид, образованный из отрезка проволоки, имеет 80 витков. Соленоид несет
постоянный ток 13 А
и сила создаваемого магнитного поля измеряется как
7,3×10 Т
в его центре. Вычислите длину соленоида, ответив на вопрос
Ближайшая
сантиметр. Используйте значение
4𝜋×10 Т⋅м/А
для 𝜇.

Ответ

Напомним, что уравнение
𝐵=𝜇𝑁𝐼𝐿
можно представить в виде, связывающем переменные с длиной соленоида:
𝐿=𝜇𝑁𝐼𝐵.

Давайте подставим полученные значения в эту форму
уравнение. Текущий
13 А, количество
витков 80, напряженность магнитного поля в центре
7,3×10 Т,
а проницаемость свободного пространства
4𝜋×10 Т⋅м/А. Это дает нам
𝐿=𝜇𝑁𝐼𝐵𝐿=4𝜋×10⋅/(80)(13)7,3×10.TmAAT

Умножая на числитель, единицы
Ампер отменить,
осталось только T⋅m:
𝐿=1,306×10⋅7,3×10.TmT

Деление этих чисел отменяет тесла,
оставляя позади только метры:
1,306×10⋅7,3×10=0,179.TmTm

Итак, длина этого соленоида равна
0,179 метра. Мы еще не закончили, так как нам нужен окончательный ответ на проблему в
сантиметры.

Чтобы выразить этот ответ в сантиметрах,
напомнить, что есть
100 сантиметров
в 1 метре:
1001.см

Умножив это на наш ответ в
метров даст
нам ответ в сантиметрах:
1001×0,179=17,9.смммсм

Итак, округляем до ближайшего
сантиметр,
этот соленоид имеет длину
18 сантиметров. Ответ 18 см.

Напомним, что длина соленоида обратно пропорциональна магнитному полю
сила в его центре. Более длинной длине можно противодействовать, добавляя больше витков в
провод, как показано на схеме ниже.

Оба соленоида имеют одинаковую напряженность магнитного поля, так как более длинный соленоид имеет
пропорционально большее количество оборотов. Мы также можем видеть, что более длинный соленоид
по сути то же самое, что и первое, но его просто больше.

Это означает, что добавление большего количества витков провода, увеличение длины соленоида в процессе,
вообще не увеличивает напряженность магнитного поля в центре. Что увеличивает
напряженность магнитного поля — это число витков на заданной длине. Это
доказано, глядя на уравнение
𝐵=𝜇𝑁𝐼𝐿.

Если предположить, что ток одинаков для двух соленоидов, то единственный
непостоянными переменными, влияющими на напряженность магнитного поля, являются число витков
𝑁 и длина 𝐿:
𝑁𝐿.

Мы видим, что удвоение витков до 2𝑁 и длины до
2𝐿 вообще не меняет эту пропорцию. Удвоенные значения
исключают друг друга:
2𝑁2𝐿=𝑁𝐿.

Для упрощения уравнения эту пропорцию часто сокращают до простой строчной буквы.
𝑛,
𝑁𝐿=𝑛,
единицами которых являются витки на единицу длины. Внутри полного уравнения это
выглядит следующим образом.

Уравнение: магнитное поле в центре соленоида с числом оборотов на
Длина блока

Напряженность магнитного поля, 𝐵, внутри центра соленоида
находится с помощью уравнения
𝐵=𝜇𝑛𝐼,
где 𝐼 — ток соленоида,
𝑛 — количество витков на единицу длины, а
𝜇 — проницаемость свободного пространства,
4𝜋×10 Т⋅м/А.

Единицы 𝑛 выражены на единицу длины. Например,
рассмотрите соленоид на диаграмме ниже.

Значение 𝑛 — это общее количество витков по всей длине:
𝑛=𝑁𝐿.

Итак, 6 витков и 3 см
длины дает
63=2.turnscmturnspercentimetre

Если бы мы удвоили количество витков до 12 и удвоили длину до
6 см, мы бы увидели значение
𝑛 все тот же
126=2.оборотсмоборотовпроцентиметр

Только путем изменения пропорции витков к длине соленоида
изменение напряженности магнитного поля.

Давайте рассмотрим пример.

Пример 4: Изменения магнитного поля в соленоиде

Отрезок проволоки превращается в соленоид с 𝑛
витков провода на
миллиметр. По проводу течет постоянный ток 𝐼. В результате магнитное поле напряженностью 𝐵 может быть
измеряется в центре соленоида. Какое из следующих изменений в системе увеличит магнитное
напряженность поля в центре соленоида, при условии, что все остальное
остается постоянным?

1. Уменьшение длины соленоида путем удаления витков провода при
   сохраняя 𝑛 постоянным
2. Уменьшая 𝐼, ток в проводе
3. Уменьшая 𝑛, количество витков провода на
   миллиметр
4. Увеличение 𝐼, тока в проводе
5. Увеличение длины соленоида добавлением витков провода при
   сохраняя 𝑛 постоянным

Ответ

Вспомним форму уравнения с
𝑛 оборотов на единицу длины:
𝐵=𝜇𝑛𝐼. 

Если 𝑛 не изменяется в этом уравнении, магнитное поле
сила не меняется. Добавление или удаление частей соленоида, но
сохранение постоянной 𝑛 означает напряженность магнитного поля
остается такой же.

Уменьшение 𝑛, однако, уменьшит магнитное поле
прочность. Точно так же уменьшение тока также уменьшит магнитное поле.
напряженность поля. Это связано с тем, что напряженность магнитного поля напрямую
пропорциональна как 𝑛, так и 𝐼.

Единственный способ увеличить напряженность магнитного поля — увеличить
𝑛 или 𝐼. Единственный ответ с этим
увеличение D, увеличение 𝐼.

Правильный ответ D, при увеличении тока в проводе будет увеличиваться
напряженность магнитного поля.

При использовании 𝑛 для выполнения вычислений обороты безразмерны,
поэтому единицы 𝑛 указаны только на единицу длины. Это означает, что
хотя мы бы сказали 5 оборотов в
метр,
внутри уравнения мы бы просто написали
5. м

Давайте рассмотрим пример.

Пример 5: Напряженность магнитного поля в центре соленоида

Провод, по которому течет постоянный ток
0,15 А
представляет собой соленоид с 11 витками на
сантиметр. Вычислите напряженность магнитного поля в центре
соленоид. Дайте свой ответ в
тесла
выражается в научной записи с точностью до одного десятичного знака. Используйте значение
4𝜋×10 Т⋅м/А
для 𝜇.

Ответ

Соленоид выглядит так, как показано на рисунке ниже.

Вспомните уравнение для напряженности магнитного поля в центре
соленоид с использованием оборотов на единицу длины:
𝐵=𝜇𝑛𝐼.

Прежде чем подставлять значения в это уравнение, мы должны убедиться, что
единицы совпадают. Проницаемость использования свободного пространства
метры,
поэтому нам нужно поставить 𝑛 с точки зрения
метров также.

Значение 𝑛 составляет 11 витков на
сантиметр,
а там 100 сантиметров
в 1 метре:
1001.см

Умножив это соотношение на 11 витков на
сантиметр
превратит его в число оборотов в
метр:
1001×11=1100.cmcmm

Теперь мы можем подставить значения в уравнение. Текущий
0,15 А,
𝑛 составляет 1‎ ‎100 оборотов в
метр,
и 𝜇
4𝜋×10 Т⋅м/А. Это дает нам
𝐵=𝜇𝑛𝐼𝐵=4𝜋×10⋅/1100(0,15).TmAmA

Умножая проницаемость свободного пространства на обороты на
метр
отменяет счетчики,
оставляя позади
𝐵=1,38×10/(0,15).ТАА

Умножение двух последних чисел отменяет единицы измерения.
ампер,
оставив тесла, чтобы дать
1,38×10/(0,15)=2,07×10,TAAT

Таким образом, округляя до одного десятичного знака, напряженность магнитного поля в
центр этого соленоида
2,1×10 T.

Как и в случае с другой версией уравнения напряженности магнитного поля, мы можем
изолировать конкретные неизвестные переменные. Например, если нам дан соленоид с
неизвестный ток, мы можем определить его, составив уравнение
𝐵=𝜇𝑛𝐼
с точки зрения 𝐼.

Для этого разделим обе части на 𝜇𝑛:
𝐵𝜇𝑛=𝜇𝑛𝐼𝜇𝑛.

Отменяет 𝜇𝑛 с правой стороны, оставляя позади
только 𝐼:
𝐵𝜇𝑛=𝐼.

Давайте рассмотрим пример, в котором используется эта форма уравнения.

Пример 6: Определение тока в соленоиде с количеством витков на длину

Соленоид состоит из отрезка провода, по которому течет постоянный ток
𝐼. Соленоид имеет 430 витков провода на
метр. Магнитное поле в центре соленоида измеряется как
3,2×10 Т. Рассчитаем ток, 𝐼,
в амперах. Дайте ответ с точностью до 1 знака после запятой. Использовать
𝜇=4𝜋×10⋅/TmA.

Ответ

Напомним, что уравнение
𝐵=𝜇𝑛𝐼
можно выразить в терминах 𝐼 следующим образом:
𝐼=𝐵𝜇𝑛. 

Используя эту форму, подставим известные значения. Напряженность магнитного поля
3,2×10 Т,
𝑛 составляет 430 витков на метр,
и 𝜇
4𝜋×10 Т⋅м/А. Это дает нам
𝐼=𝐵𝜇𝑛𝐼=3,2×10(4𝜋×10⋅/).TTmAm

Умножение на знаменатель удаляет единицы
метров, дача
𝐼=3,2×105,4×10/.ТТА

Деление на дробь равносильно умножению на ее обратную величину. Это означает, что единственным юнитом после деления будет
ампер:
ТТАТАТА/=×=.

Итак, при делении чисел ответ становится
3,2×105,4×10/=5,92.TTAA

Округлив до ближайшего десятичного знака, ответ будет
5.9 A.

Давайте обобщим то, что мы узнали из этого объяснения.

Основные положения

• Соленоид представляет собой провод, состоящий из ряда витков или петель.
• Когда по соленоиду течет ток, он создает магнитное поле, которое
  сильнее всего в центре своих петель.
• В петлях соленоида напряженность магнитного поля 𝐵
  дается уравнением
  𝐵=𝜇𝑁𝐼𝐿,
  где 𝑁 — число витков в соленоиде,
  𝐼 — ток в соленоиде, 𝐿 —
  длина соленоида, а 𝜇 — проницаемость свободной
  пространство, 4𝜋×10 Т⋅м/А.
• Уравнение для напряженности магнитного поля 𝐵 в центре
  соленоид с использованием оборотов на единицу длины
  𝐵=𝜇𝑛𝐼,
  где 𝑛 — количество витков на единицу длины,
  𝐼 — ток соленоида, а
  𝜇 — проницаемость свободного пространства,
  4𝜋×10 Т⋅м/А.

Соленоид Определение и значение — Merriam-Webster

так · ле · ноид

ˈsō-lə-ˌnȯid 

ˈsä-

: катушка из проволоки, обычно цилиндрической формы, которая при протекании тока действует как магнит, так что подвижный сердечник втягивается в катушку, когда течет ток, и который используется особенно в качестве переключателя или элемента управления для механического устройства (например, клапана)

соленоидальный

ˌsō-lə-ˈnȯi-dᵊl 

ˌsä-

имя прилагательное

Примеры предложений

Недавние примеры в Интернете

Насосная смена 9Соленоид 0291 может подвергнуться внутренней коррозии, что приведет к потере питания модуля управления насосом.

Detroit Free Press , 21 августа 2021 г.

Вторая, более распространенная проблема — плохой соленоид в манетке в сборе.

Мотормут Боб Вебер, Star Tribune , 9 июля 2021 г.

Заменить соленоид 9 продувки паров топлива 0292 : 149 долларов.

Джим Горзелани, Forbes , 27 апреля 2021 г.

Кроме того, 18 катушек тороидального поля будут окружать машину по вертикали, а один большой центральный соленоид будет располагаться посередине, образуя самую большую сверхпроводящую магнитную систему из когда-либо построенных.

Клара Московиц, Scientific American , 1 декабря 2020 г.

Джетограф Пол Уилер, ветеран звуковой фотографии с восьмилетним стажем, установил на свой Speed ​​Graphic более мощную пружину, более мощную 9-дюймовую пружину. 0291 соленоид — для предотвращения преждевременного срабатывания затвора перегрузкой.

Джеймс Джозеф, Popular Mechanics , 31 декабря 2020 г.

Шесть модулей, каждый высотой 7 футов, диаметром 14 футов и весом 250 000 фунтов, будут установлены друг на друга для создания соленоида .

Роб Николевски, San Diego Union-Tribune , 6 ноября 2020 г.

Рабочие, ученые и инженеры General Atomics изготавливают соленоид в виде отдельных модулей, которые будут отправлены во Францию ​​и собраны.

Роб Николевски, San Diego Union-Tribune , 6 ноября 2020 г.

Если выключатель стоп-сигнала не отрегулирован, нажатие на педаль не приведет к освобождению соленоида блокировки переключения передач на механизме переключения передач.

Боб Вебер, chicagotribune.com , 17 июня 2017 г.

Узнать больше

Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «соленоид». Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.

История слов

Этимология

французский solénoïde , от греческого sōlēnoeidēs трубчатый, от греческого sōlēn труба

Первое известное использование

1827, в значении, определенном выше

Путешественник во времени

Первое известное использование соленоида было
в 1827 г.

Посмотреть другие слова того же года
соленоглифический

соленоид

электромагнитный тормоз

Посмотреть другие записи поблизости

Процитировать эту запись
«Соленоид».

Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/solenoid. По состоянию на 17 ноября 2022 г.

Copy Citation

Детское определение

Соленоид

так · ле · ноид

ˈsō-lə-ˌnȯid 

ˈsäl-ə-

: катушка из проволоки, обычно имеющая форму длинного цилиндра, который при прохождении тока действует как магнит, так что подвижный сердечник втягивается в катушку при протекании тока

Еще от Merriam -Webster о соленоиде

Britannica.