Планетарный ряд: Планетарный механизм | это… Что такое Планетарный механизм?

Планетарный механизм | это… Что такое Планетарный механизм?

Планетарная передача в режиме повышения скорости. Водило (зелёное) вращается внешним источником. Усилие снимается с солнечной шестерни (жёлтая), в то время как кольцевая шестерня (красная) закреплена неподвижно. Красные метки показывают вращение входного вала на 45°.

Планетарная передача — механическая система, состоящая из нескольких планетарных зубчатых колёс (шестерён), вращающихся вокруг центральной, солнечной, шестерни. Обычно, планетарные шестерни фиксируются вместе с помощью водила. Планетарная передача может также включать дополнительную внешнюю кольцевую шестерню, имеющую внутреннее зацепление с планетарными шестернями.

Передаточное отношение

Водило (зелёное) закреплено неподвижно, в то время как солнечная шестерня (жёлтая) вращается внешним источником. В данном случае передаточное отношение равно -24/16, или -3/2; каждая планетарная шестерня поворачивается на 3/2 оборота относительно солнечной шестерни, в противоположном направлении.

Передаточное отношение такой передачи визуально определить достаточно сложно, в основном, потому что система может приводиться во вращение несколькими разными способами. Основными элементами планетарной передачи можно считать следующие:

• Солнечная шестерня: находится в центре;
• Водило: жёстко фиксирует друг относительно друга оси нескольких планетарных шестерён (сателлитов) одинакового размера, находящихся в зацеплении с солнечной шестерней;
• Кольцевая шестерня (эпицикл): внешнее зубчатое колесо, имеющее внутреннее зацепление с планетарными шестернями.

При использовании планетарной передачи в качестве редуктора один из трёх её основных элементов фиксируется неподвижно, другой элемент используется как ведущий, а третий – в качестве ведомого. Таким образом, передаточное отношение будет зависеть от количества зубьев каждого компонента, а также того, какой элемент закреплён.

Часто планетарные передачи используются для суммирования двух потоков мощности (например, планетарные ряды двухпоточных трансмиссий некоторых танков и др. гусеничных машин), в этом случае неподвижно зафиксированных элементов нет. Например, два потока мощности могут подводиться к солнечной шестерне и эпициклу, а результирующий поток снимается с водила.

Рассмотрим случай, когда водило зафиксировано, а мощность подводится через солнечную шестерню. В этом случае планетарные шестерни вращаются на месте со скоростью, определяемой отношением числа их зубьев относительно солнечной шестерни. Например, если мы обозначим число зубьев солнечной шестерни как S, а для планетарных шестерён примем это число как P, то передаточное отношение будет определяться формулой —S/P, то есть если у солнечной шестерни 24 зуба, а у планетарных по 16, то передаточное отношение будет -24/16, или -3/2, что означает поворот планетарных шестерён на 1,5 оборота в противоположном направлении относительно солнечной.

Далее вращение планетарных шестерён может передаваться кольцевой шестерне, с соответствующим передаточным числом. Если кольцевая шестерня имеет A зубьев, то оно будет вращаться с соотношением P/A относительно планетарных шестерён. (В данном случае перед дробью нет минуса, так как при внутреннем зацеплении шестерни вращаются в одну сторону). Например, если на кольцевой шестерне 64 зуба, то относительно приведённого выше примера это отношение будет равно 16/64, или 1/4. Таким образом, объединив оба примера, мы получим следующее:

• Один оборот солнечной шестерни даёт —S/P оборотов планетарных шестерён;
• Один оборот планетарной шестерни даёт P/A оборотов кольцевой.

В итоге, если водило заблокировано, общее передаточное отношение системы будет равно —S/A.

В случае, если закреплена кольцевая шестерня, а мощность подводится к водилу, передаточное отношение на солнечную шестерню будет больше единицы и составит 1+A/S.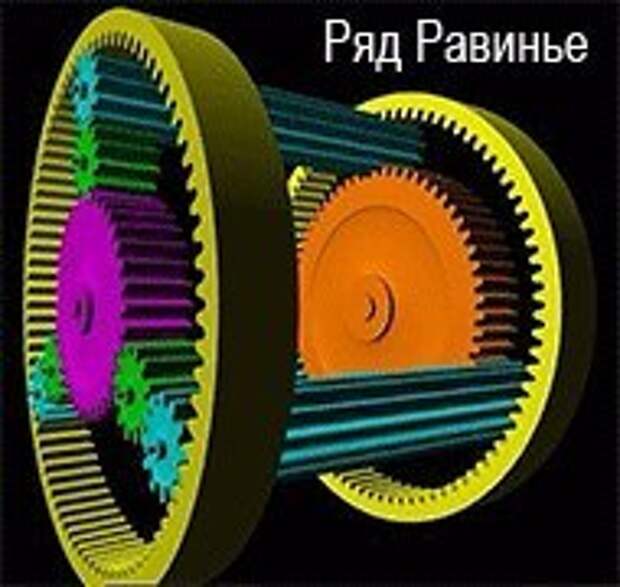

Всё вышесказанное можно описать следующим выражением:

,

где n – это параметр передачи, равный , то есть отношению числа зубьев солнечной и планетарных шестерён.

Если закрепить кольцевую шестерню, а мощность подводить к солнечной шестерне, то мощность должна сниматься с водила. В этом случае передаточное отношение будет равно 1/(1+A/S). Это самое маленькое передаточное число, которое может быть получено в планетарной передаче. Такие передачи используются, например, в тракторах и строительной технике, где требуется большой крутящий момент на колёсах при невысокой скорости.

Применение

Наиболее широкое применение принцип нашёл в автомобильных дифференциалах, кроме того используется в суммирующих звеньях кинематических схем металлорежущих станков.

В современных устройствах могут использоваться каскады из нескольких планетарных передач для получения большого диапазона передаточных чисел. На этом принципе работают многие автоматические коробки передач.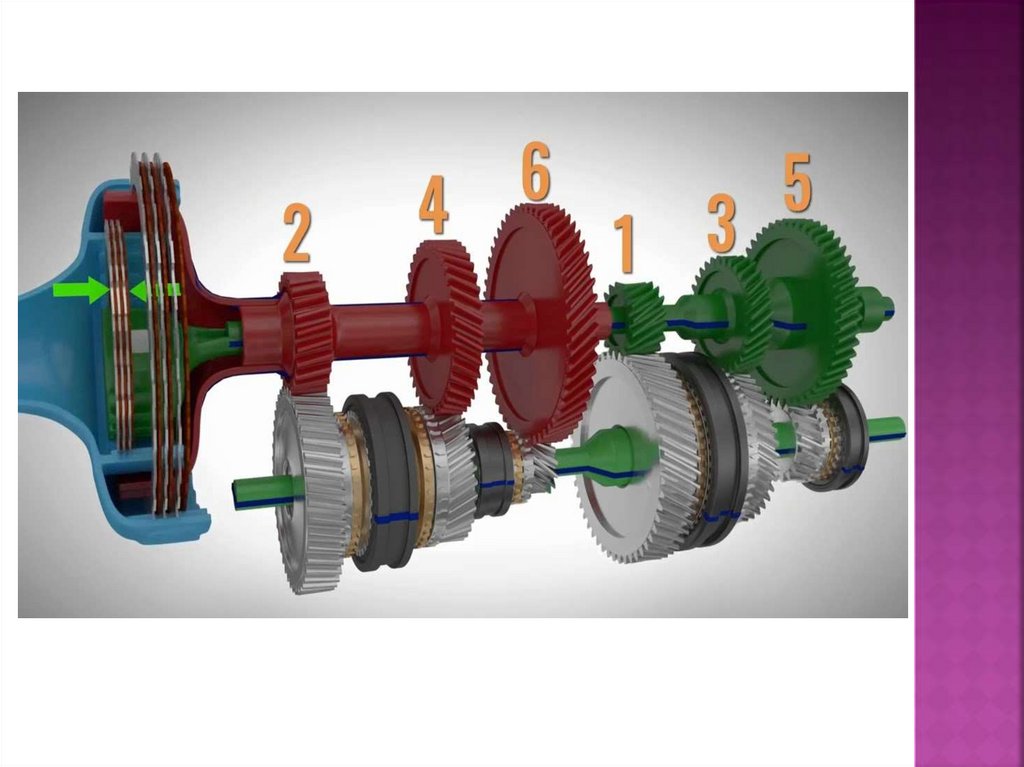

Во время Второй мировой войны была разработана особая конструкция планетарной передачи, которая использовалась для привода небольших радаров. Кольцевая шестерня изготавливалась из двух частей, каждая толщиной в половину толщины других компонентов. Одна из этих половинок фиксировалась неподвижно и имела на 1 зуб меньше, чем вторая. В такой конструкции при полном обороте планетарных шестерён и нескольких оборотах солнечной шестерни, подвижное кольцо поворачивалось всего на 1 зуб. Таким образом, получалось очень высокое передаточное отношение при небольших габаритах.

Cм. также

• механический редуктор
• Зубчатые передачи
• Автоматическая трансмиссия
• Передача Симпсона

коробка, механизм, шестерня, ряд и расчет

Планетарная передача — вид зубчатой передачи, применяемой в механических и автоматических трансмиссиях. Помимо преобразования вращения «планетарка» способна суммировать и раскладывать мощности. Зная о планетарном механизме: что это такое, как работает, по каким критериям оценивают редуктор, станет понятно устройство и характеристики АКПП. В случае поломки расчёт передачи поможет выбрать надёжный и долговечный механизм.

Содержание

1. Устройство и принцип работы
2. Разновидности планетарных передач
3. Характеристики основных разновидностей этого устройства
4. Цилиндрические
5. Конические
6. Волновые
7. Достоинства и недостатки планетарных передач
8. Передаточное число планетарных передач
9. Подбор чисел зубьев планетарных передач
10. Расчет на прочность планетарных передач
11. Советы по подбору планетарного редуктора
12. Область применения планетарных передач
13. Заключение

Устройство и принцип работы

Планетарный механизм — это конструкция из зубчатых колёс, перемещающихся относительно центра. По центральной оси расположены колёса разного диаметра:

• малое солнечное с внешними зубцами;
• большое коронное или эпицикл с внутренними зубцами.

Между колёсами передвигаются сателлиты. Их вращение напоминает движение планет Солнечной системы. Оси сателлитов механические соединены на водиле, которое вращается относительно центральной оси.

Устройство простого планетарного блока:

• 1 эпицикл;
• 1 солнечное колесо;
• 1 водило.

Планетарный механизм собирают в каскады из двух и более звеньев на одном валу для получения широкого диапазона передач. Главной кинематической характеристикой зубчатой передачи является передаточное отношение.

Принцип работы планетарной коробки заключается в блокировке одного из основных элементов и передаче вращения через ведущее колесо. Для остановки элемента применяют тормозные ленты, блокировочные муфты, конические шестерни. Передаточное отношение меняется в зависимости от схемы закрепления. Описать принцип действия планетарного механизма удобнее на примере:

1. Корона блокируется.
2. Вал подаёт крутящий момент на солнце.
3. Вращение солнца заставляет планеты обкатываться вместе с ним.
4. Водило становится ведомым, сообщая пониженную передачу.

Управляя элементами простой «планетарки», получают разные характеристики:

Передача	Как работает планетарная коробка в АКПП
1	Солнце подаёт вращение на водило, корона двигается в противоположную сторону.
2	Корона подаёт вращение на водило, солнце зафиксировано.
3	Ведущее водило передаёт вращение солнцу. Корона заблокирована.
4	Водило двигает корону. Солнце зафиксировано.
Задний ход	Водило заблокировано. Солнечное колесо вращается, планеты обкатывают и двигают корону в противоположную сторону.

Кпд η простой передачи достигает 0,97.

Планетарный ряд с одной степенью свободы становится планетарной передачей. Две степени образуют дифференциал. Дифференциал складывает моменты на ведомом колесе, поступающие от основных ведущих звеньев.

Разновидности планетарных передач

По количеству ступеней планетарные механизмы разделяют на:

• однорядные;
• многорядные.

Планетарная передача из одной солнечной шестерни, одновенцовых сателлитов, водила и эпицикла будет однорядной. Замена сателлитов на двухвенцовые усложняет конструкцию, делая её двухрядной.

Многоступенчатая планетарная коробка передач — это последовательно установленные однорядные блоки. Такая схема позволяет суммировать передаточные числа и получать большие значения. 4-скоростные АКПП состоят из двухрядных планетарных конструкций, 8-скоростные — из четырёхрядных.

В АКПП применяют схемы, названные в честь изобретателей:

• Механизм Уилсона представляет собой трёхрядную конструкцию, в которой соединены корона первого, водило второго и корона третьего рядов. Количество передач — 5 прямых и 1 задняя.
• Механизм Лепелетье состоит из 3 соосно расположенных простых планетарных передач. Количество передач — 6 прямых и 1 задняя.
• Схема Симпсона — 2 редуктора с общей солнечной шестернёй. Водило второго ряда оборудовано тормозом. Корона первого ряда и солнце через две блокировочные муфты жёстко соединены с ведущим валом. Механизм реализует режимы: нейтраль; 1,2,3 передачи; задний ход.

По типу зубчатых конструкций планетарные редукторы делятся на:

• цилиндрические;
• конические;
• волновые;
• червячные.

Разные типы применяют для передачи момента между валами, расположенными параллельно или под углом. А также в механизмах, требующих низкой или высокой кинематической характеристики.

Характеристики основных разновидностей этого устройства

В конструкции планетарного ряда АКПП применяют различные типы зубчатых передач. Выделяют три основные наиболее распространенные: цилиндрические, конические и волновые.

Цилиндрические

Зубчатые механизмы передают момент между параллельными валами. В конструкцию цилиндрической передачи входит две и более пар колёс. Форма зубьев шестерней может быть прямой, косой или шевронной. Цилиндрическая схема простая в производстве и действии. Применяется в коробках передач, бортовых редукторах, приводах. Передаточное число ограничено размерами механизма: для одной колёсной пары достигает 12. КПД — 95%.

Конические

Колёса в конической схеме преобразуют и передают вращение между валами, расположенными под углом от 90 до 170 градусов. Зубья нагружены неравномерно, что снижает их предельный момент и прочность. Присутствие сил на осях усложняет конструкцию опор. Для плавности соединения и большей выносливости применяют круговую форму зубьев.

Производство конических передач требует высокой точности, поэтому обходится дорого. Угловые конструкции применяются в редукторах, затворах, фрезерных станках. Передаточное отношение конических механизмов для техники средней грузоподъёмности не превышает 7. КПД — 98%.

Волновые

Во волновой передаче отсутствуют солнечная и планетные шестерни. Внутри коронного колеса установлено гибкое зубчатое колесо в форме овала. Водило выступает в качестве генератора волн, и выглядит в виде овального кулачка на специальном подшипнике.

Гибкое стальное или пластмассовое колесо под действием водила деформируется. По большой геометрической оси зубья сцепляются с короной на всю рабочую высоту, по малой оси зацепление отсутствует. Движение передаётся волной, создаваемой гибким зубчатым колесом.

Во волновых механизмах КПД растёт вместе с передаточным числом, превышающим 300. Волновая передача не работает в схемах с кинематической характеристикой ниже 20. Редуктор выдает 85% КПД, мультипликатор — 65%. Конструкция применяется в промышленных роботах, манипуляторах, авиационной и космической технике.

Планетарная передача выигрывает у простых зубчатых механизмов аналогичной мощности компактным размером и массой меньшей в 2 — 3 раза. Используя нескольких планетных шестерней, достигается зацепление зубьев на 80%. Нагрузочная способность механизма повышается, а давление на каждый зубец уменьшается.

Кинематическая характеристика планетарного механизма доходит до 1000 с малым числом зубчатых колёс без применения многорядных конструкций. Помимо передачи планетарная схема способна работать как дифференциал.

За счёт соосности валов планетарного механизма, компоновать машины проще, чем с другими редукторами.

Применение планетарного ряда в АКПП снижает уровень шума в салоне автомобиля. Сбалансированная система имеет высокую вибропрочность за счет демпфирования колебаний. Соответственно снижается вибрация кузова.

Недостатки планетарного механизма:

• сложное производство и высокая точность сборки;
• в сателлиты устанавливают подшипники, которые выходят из строят быстрее, чем шестерня;
• при повышении передаточных отношений КПД падает, поэтому приходится усложнять конструкцию.

Передаточное число планетарных передач

Передаточным называют отношение частоты ведущего вала планетарной передачи к частоте ведомого. Визуально определить его значение не получится. Механизм приводится в движение разными способами, а значит передаточное число в каждом случае различно.

Для расчёта передаточного числа планетарного редуктора учитывают число зубьев и систему закрепления. Допустим, у солнечной шестерни 24 зуба, у сателлита — 12, у короны — 48. Водило закреплено. Ведущим становится солнце.

Сателлиты начнут вращаться со скоростью, передаваемой солнечной шестернёй. Передаточное отношение равно: -24/12 или -2. Результат означает, что планеты вращаются в противоположном направлении от солнца с угловой скоростью 2 оборота. Сателлиты обкатывают корону и заставляют её обернуться на 12/48 или ¼ оборота. Колёса с внутренним закреплением вращаются в одном направлении, поэтому число положительное.

Общее передаточное число равно отношению числа зубьев ведущего колеса к количеству зубьев ведомого: -24/48 или -1/2 оборота делает корона относительно солнца при зафиксированном водиле.

Если водило станет ведомым при ведущем солнце, то передаточное отношение: (1+48/24) или 3. Это самое большое число, какое способна предложить система. Самое маленькое отношение получается при фиксировании короны и подачи момента на водило: (1+/(1+48/24)) или 1/3.

Передаточные числа простой планетарной схемы: 1,25 — 8, многоступенчатой: 30 — 1000. С ростом кинематической характеристики КПД снижается.

Подбор чисел зубьев планетарных передач

Число зубьев колёс подбирают на первом этапе расчёта планетарной схемы по заранее установленному передаточному отношению. Особенность проектирования планетарного ряда заключается в соблюдении требований правильной сборки, соосности и соседства механизма:

• зубья сателлитов должны совпадать с впадинами солнца и эпицикла;
• планеты не должны задевать друг друга зубьями. На практике более 6 сателлитов не используют из-за трудностей равномерного распределения нагрузки;
• оси водила, солнечного и коронного колёс должны совпадать.

Основное соотношение подбора зубьев передачи через передаточное число выглядит так:

i = 1+Zкорона/Zсолнце,

где  i — передаточное число;

Zn — количество зубьев.

Условие соосности соблюдается при равных межосевых расстояниях солнечного колеса, короны и водила. Для простой планетарной зубчатой передачи проверяют межосевые расстояния между центральными колёсами и сателлитами. Равенство должно удовлетворять формуле:

Zкорона= Zсолнце+2×Zсателлит.

Чтобы между планетами оставался зазор, сумма радиусов соседних шестерней не должна превышать осевое расстояние между ними. Условие соседства с солнечным колесом проверяют по формуле:

sin (π/c)> (Zсателлит+2)/(Zсолнце+Zсателлит),

где с — количество сателлитов.

Планетные колёса размещаются равномерно, если соотношение зубьев короны и солнца к количеству сателлитов окажется целым:

Zсолнце/с = Z;

Zкорона/с = Z,

где Z — целое число.

Расчет на прочность планетарных передач

Прочностной расчёт планетарных передач проводят как для цилиндрических зубчатых передач. Вычисляют каждое зацепление:

• внешнее — между солнцем и планетными колёсами;
• внутреннее — между планетами и короной.

Если колёса изготовлены из одного материала, а силы в зацеплении равны, рассчитывают наименее прочное соединение — внешнее.

Алгоритм расчёта следующий:

1. Выбирают схему редуктора.
2. Определяют исходные данные: передаточное число i, крутящий момент Твых и частоту вращения выходного вала Uвых.
3. Подбирают число зубьев с проверкой условий сборки и соседства планетных шестерней.
4. Рассчитывают угловые скорости колёс.
5. Вычисляют КПД и моменты выходных валов.
6. Рассчитывают прочность зацепления.

В расчёте момента учитывают количество планетных колёс и неравномерное нагружение их зубьев. 3)/(Ψ×d) ≤ [σн]

При расчёте на изгиб принимают условие, что вся нагрузка передаётся одной паре зубьев и приложена к его вершине. Расчётное напряжение не должно превышать допускаемое:

σf= (M/W) – (F/(b×s) ≤ [σf],

где М — изгибающий момент;

W — осевой момент сопротивления;

F — сила сжатия;

b, s — размеры зуба в сечении;

[σf] — допускаемое напряжение изгиба. Зависит от предела выносливости, шероховатости, погрешности изготовления зубьев.

Советы по подбору планетарного редуктора

Перед выбором планетарного редуктора проводят точный расчёт нагружения и режимов работы механизма. Определяют тип передачи, осевые нагрузки, температурный диапазон и типоразмеры редуктора. Для тяжёлой спецтехники, где нужен большой крутящий момент при малых скоростях, выбирают редуктор с высоким передаточным отношением.

Чтобы сбавить угловую скорость, не снижая крутящего момента, применяют привод с электродвигателем и редуктором. При выборе мотор редуктора учитывают:

• эксплуатационную нагрузку;
• момент вала на выходе;
• частоту вращения входного и выходного валов;
• мощность электродвигателя;
• монтажное исполнение.

Область применения планетарных передач

Планетарная схема используется в:

• редукторах;
• автоматических и механических коробках передач;
• в приводах летательных аппаратов;
• дифференциалах машин, приборов;
• ведущих мостах тяжёлой техники;
• кинематических схемах металлорежущих станков.

Планетарную коробку передач применяют в агрегатах с переменным передаточным отношением, затормаживая водило. В гусеничной технике для сложения потоков мощности элементы в планетарном механизме не блокируют.

Заключение

Планетарные передачи в АКПП зарекомендовали себя десятилетиями эксплуатации со времён Ford T: компактными размерами, малым весом, высокими скоростями, надёжностью и выносливостью. Планетарная схема способна передавать вращение и управлять потоками мощности, поэтому нашла применение в авиации, машиностроении, промышленности.

Чтобы не ошибиться с выбором конструкции, проводят точный расчёт геометрии и прочности зубчатой передачи, сверяя с допустимыми значениями. Ошибки вычислений приводят к чрезмерной нагрузке зубчатых передач, поломке и истиранию зубьев.

Основы планетарных зубчатых передач

На первый взгляд планетарные зубчатые передачи, также известные как планетарные зубчатые передачи, кажутся довольно сложными. Безусловно, требуется опытный инженер-редуктор, чтобы овладеть всеми сложными аспектами конструирования этого типа зубчатой ​​передачи. Если вы продвинутый инженер по редукторам, этот пост не для вас. Но если вы ищете более общее представление о планетарных передачах, вы попали в нужное место.

Что такое планетарные передачи?

Планетарная передача состоит из трех типов шестерен: солнечной шестерни, планетарной шестерни и зубчатого венца. Солнечная шестерня расположена в центре (желтая) и передает крутящий момент на планетарные шестерни (синие), которые обычно устанавливаются на подвижном водиле (зеленые). Планетарные шестерни вращаются вокруг солнечной шестерни и входят в зацепление с внешним зубчатым венцом (розовый). Планетарные зубчатые передачи могут различаться по сложности от очень простых до сложных составных систем, в зависимости от области применения.

Изображение предоставлено Википедией

Где используются системы планетарной передачи?

Планетарные передачи часто используются, когда важны пространство и вес, но требуется значительное снижение скорости и крутящего момента. Это требование относится к различным отраслям, включая тракторы и строительную технику, где для привода колес требуется большой крутящий момент. Другие места, где вы найдете планетарные редукторы, включают турбинные двигатели, автоматические коробки передач и даже электрические шуруповерты.

Планетарные передачи способны создавать большой крутящий момент, поскольку нагрузка распределяется между несколькими планетарными передачами. Такое расположение также создает больше контактных поверхностей и большую площадь контакта между шестернями, чем традиционная система зубчатых колес с параллельными осями. Благодаря этому в нем более равномерно распределяется нагрузка и поэтому шестерни более устойчивы к повреждениям.

Производство планетарных шестерен

Навыки, необходимые для производства планетарных шестерен, такие же, как и для любого другого типа производства прецизионных шестерен. Gear Motions — ведущий производитель прецизионных зубчатых колес, специализирующийся на поставке нарезных и шлифованных зубчатых колес на заказ. У нас есть обширный портфель возможностей производства зубчатых колес, который включает в себя возможность производить все отдельные зубчатые колеса, составляющие систему планетарных передач. Чтобы узнать о конкретных производственных возможностях, таких как минимальный и максимальный диаметр, средний диаметр и ширина торца, посетите нашу страницу возможностей производства зубчатых колес. Обратите внимание, что мы не производим редукторы.

Компания Gear Motions также имеет большой опыт в разработке и проектировании зубчатых передач. Независимо от того, нужно ли вам спроектировать систему зубчатых передач с нуля или вам нужна помощь в изменении конструкции, мы будем работать с вами на протяжении всего процесса, чтобы гарантировать, что ваши шестерни спроектированы и изготовлены с точностью. Инженерные услуги включают обратное проектирование, проектирование для технологичности, прототипирование и модернизацию.

Дополнительная информация

Для получения более подробной информации о планетарных передачах мы рекомендуем следующие ресурсы:

• Американская ассоциация производителей зубчатых колес (AGMA)

AGMA часто предлагает образовательные курсы, поддерживающие профессиональное развитие работников зубообрабатывающей промышленности. Один из недавно предложенных курсов посвящен проектированию планетарных передач. Посетите веб-сайт AGMA, чтобы узнать о текущих предложениях курсов.

• Gear Talk с Чаком

Gear Talk with Chuck — блог, написанный Чарльзом Д. Шульцем для Gear Technology. Если вы активно работаете в индустрии передач, вы, вероятно, уже знакомы с ней. Gear Talk недавно опубликовал серию сообщений в блоге о планетарных передачах. Содержание основано на многолетнем опыте Шульца в зубообрабатывающей промышленности и содержит значительный объем технических знаний. Если вы ищете информацию о планетарных передачах с уникальной точки зрения, обязательно ознакомьтесь с серией.

У вас есть конкретные вопросы по проектированию или производству планетарной передачи? Свяжитесь с Gear Motions! Наши инженеры по продажам будут работать с вами от начала до конца, чтобы убедиться, что ваш проект выполнен в соответствии с вашими требованиями.

См. Возможности Gear

Планетарная зубчатая передача — Rohloff AG

Планетарная трансмиссионная система (или планетарная система, как она также известна) обычно состоит из центральной солнечной шестерни, зубчатого венца и нескольких планетарных шестерен, которые вращаются между ними.

Эта концепция сборки объясняет термин планетарная передача, так как планетарные шестерни вращаются вокруг солнечной шестерни, как в астрономическом смысле планеты вращаются вокруг нашего солнца.

Преимущество планетарной передачи определяется распределением нагрузки между несколькими планетарными шестернями. Таким образом, можно передавать высокие крутящие моменты, используя компактную конструкцию.

Узел шестерни 1 и узел шестерни 2 Rohloff SPEEDHUB 500/14 имеют две выбираемые солнечные шестерни. Первая ступень ступенчатой ​​планетарной шестерни входит в зацепление с солнечной шестерней №1. Вторая ступень шестерни входит в зацепление с солнечной шестерней №2. При соединении солнечной шестерни 1 или 2 с осью или при соединении солнечной шестерни 1 с зубчатым венцом возможны три варианта передаточного числа для каждого зубчатого колеса в сборе.

Пример шестерни в сборе (1) и (2)

Если в шестерне в сборе (1) или (2) выбрана прямая передача, солнечная шестерня 1 соединена с зубчатым венцом в шестерне в сборе (1) или шестерне в сборе (2) ) соответственно. Солнечная шестерня 1 и зубчатый венец затем вращаются вместе с одинаковой скоростью. Ступенчатые планетарные шестерни не раскручиваются. Таким образом, передаточное число составляет 1:1.

Шестерня в сборе (3) требует прямой передачи по тому же принципу. Солнечная шестерня 3 и зубчатый венец 3 соединены напрямую.

Пример узла шестерни №1

Входной сигнал от узла шестерни (1) передается через зубчатый венец. Когда солнечная шестерня 1 соединена с осью, первая ступень ступенчатой ​​планетарной шестерни проходит между неподвижной солнечной шестерней 1 и вращающимся зубчатым венцом. Один оборот зубчатого венца (зеленая стрелка) соответствует 0,682 оборота водила планетарной передачи (красная стрелка).

Пример узла шестерни № 2

В этом случае узла шестерни № 2 вход передается через водило планетарной передачи, а выход передается через зубчатый венец. Таким образом, соотношение вращения меняется на противоположное по сравнению с шестерней в сборе №1. Водило планетарной передачи (красная стрелка) совершает 0,682 полного оборота, что приводит к одному полному обороту зубчатого венца (зеленая стрелка), когда солнечная шестерня №1 соединена с осью.

Пример узла шестерни № 1

Входной сигнал от узла шестерни № 1 передается через зубчатый венец.