Для чего нужен дифференциал: что это, значение, принцип работы

ЧТО ТАКОЕ ДИФФЕРЕНЦИАЛ И КАК ОН РАБОТАЕТ?

Дифференциал в автомобиле работает с целью осуществления следующих трёх задач:

• Дифференциал передаёт мощность двигателя на колёса машины.
• Делает последний шаг в уменьшении числа оборотов к колёсам (мы ведь помним, что первый такой шаг делает коробка передач) и, следовательно, увеличивая крутящий момент, передаваемый тем же ведущим колёсам.
• Передавая мощность на ведущие колёса (всегда на чётное количество колёс на одной оси: на два или на все четыре), дифференциал позволяет каждому из них вращаться с разными скоростями (это именно то, от чего дифференциал заработал своё название).

В этой статье Вы узнаете, почему Ваш автомобиль нуждается в разных оборотах вращения колёс, как это обеспечивается, что такое дифференциал, как дифференциал работает и каковы его основные недостатки. Мы также рассмотрим несколько его типов.

Для чего нужен дифференциал?

Автомобильные колёса вращаются с разной скоростью, особенно это заметно при повороте. Вы можете видеть в анимации ниже, что каждое колесо проезжает очень разное расстояние, когда автомобиль поворачивает, и что внутренние колёса проезжают гораздо более короткое расстояние, чем внешние. Поскольку скорость равна расстоянию, поделённому на время, необходимое для проезда этого расстояния, то получается, что колёса, которые проезжают меньшее расстояние, вращаются с более низкой скоростью: так, при повороте налево левые колёса будут крутиться медленнее, чем правые, и наоборот. Также следует отметить, что передние колёса проезжают расстояние, отличающееся от того, которое проезжают задние колёса.

Для автомобилей с приводом только на одну ось колёс — будь то на задние колёса или же на передние — разность вращения передних колёс к задним это не проблема. Нет никакой связи между ними, поэтому они вращаются независимо. Но ведущие колёса связаны между собой так, чтобы один двигатель и трансмиссия должны приводить в движение оба колеса, при этом, с разной скоростью их вращения. Но как же быть, если двигатель у нас всего один?! Если Ваш автомобиль не оснащён дифференциалом, колёса должны быть заблокированы вместе, будучи вынужденными вращаться с одной и той же скоростью. Это сделало бы манёвры поворотов — даже под небольшим углом — сложными: у таких автомобилей, чтобы иметь возможность повернуть, одной из шин обязательно придётся скользить, либо другой обязательно пробуксовывать. А с современными покрышками и асфальтовыми дорогами для этого потребуется достаточно много сил. Эта сила должна будет передаваться через ось от одного колеса к другому, возложив, таким образом, очень тяжёлое бремя на компоненты оси.

Именно с этой проблемой безукоризненно справляется дифференциал.

Что такое дифференциал?

Дифференциал — это устройство, которое разделяет крутящий момент двигателя на два пути с выходами, что позволяет каждому выходу вращаться с различной скоростью.

Дифференциал имеется на всех современных легковых и грузовых автомобилях, а также на многих полноприводных машинах.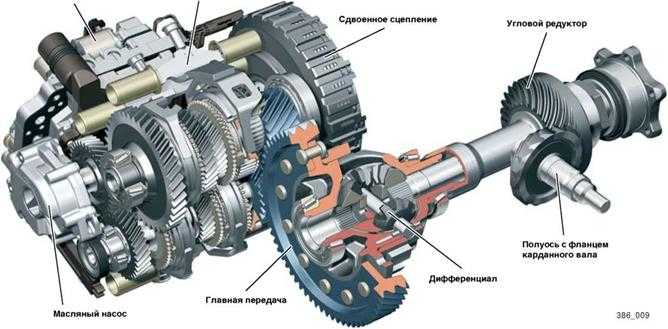 Причём, все полноприводные авто должны иметь дифференциал между каждым набором ведущих колёс на одной оси, и, кроме того, они нуждаются в дифференциале между парами передних и задних колёс (помните начало статьи — потому что передние колёса проходят другую дистанцию, в отличие от задних колёс при движении автомобиля по направлению, отличному от прямого?).

Тем не менее, некоторые полноприводные машины не имеют дифференциала между передними и задними колёсами, и, вместо этого, эти пары колёс тесно связаны между собой так, что передние и задние колёса должны крутиться с одной и той же скоростью. Вот почему на таких автомобилях производители не рекомендуют ездит по твёрдому покрытию в режиме полного привода, а включать его только на бездорожье.

А теперь давайте выясним, в каком месте автомобиля обычно располагается дифференциал в зависимости от типа привода автомобиля: 

Как работает дифференциал?

Мы начнем с простейшего типа дифференциала, называемого открытым дифференциалом. Но сначала мы должны изучить некоторые термины — посмотрите на рисунок ниже, там Вы найдёте основные компоненты работы дифференциала:

Таким образом, дифференциал состоит из следующих основных частей:

• Ведущий вал — передаёт крутящий момент, ведя его от коробки передач к началу дифференциала
• Ведущая шестерня ведущего вала — косозубая небольшая шестерня в форме конуса, которая используется для сцепки с механизмом дифференциала
• Коронная шестерня — ведомая шестерня также в форме конуса, которая приводится в движение (вращение) ведущей шестерней. Ведущая и ведомая шестерня, вместе взятые, называются главной передачей и именно они служат последним этапом уменьшения скорости вращения, которое в конечном счёте достигнет колёс (коронная шестерня всегда меньше ведущей, а, значит, ведущей шестерне придётся сделать намного больше оборотов, пока ведомая сделает всего один оборот вокруг себя).
• Шестерни полуосей — это последние шестерни на пути передачи вращения от ведущего вала к колёсам.
• Сателлиты — планетарный механизм, который как раз и осуществляет ключевую роль в обеспечении разности вращения колёс при повороте.
• Полуоси — валы, идущие от дифференциала непосредственно к колёсам.

А теперь давайте перейдём к ключевому и самому важному понимаю, как работает дифференциал, и посмотрим на анимации ниже, как вышеперечисленные компоненты открытого дифференциала работают в двух случаях:

• Когда автомобиль едет прямо.
• Когда автомобиль поворачивает.

Какой главный недостаток дифференциала?

Открытый дифференциал передаёт вращение тому или иному колесу практически в любом соотношении, в том числе и в соотношении 100%/0% — когда одно из ведущих колёс принимает весь крутящий момент на себя. В то же время распределение такого вращения между колёсами происходит при изменении нагрузки на эти колёса (а вместе с ними на полуоси) — то есть колесо с меньшей нагрузкой в повороте получает больше вращения. Но здесь кроется один существенный недостаток, который имеет место при определённых условиях, а именно, когда оба ведущих колеса находятся в грязи, снегу или на льду, и автомобиль начинает буксовать — в этом случае то колесо, которое имеет меньшее сцепление с поверхностью, будет получать львиную долю вращения. Проще говоря, если Вы, к примеру, застряли в снегу, сев «на пузо» — когда одно колесо сцеплено с поверхностью снега, а второе вовсе висит в воздухе, то получать мощность за счёт соответствующего распределения по полуосям дифференциала будет как раз то колесо, которое находится на весу, и именно оно будет беспомощно крутиться в воздухе. Особенно остро данная проблема стоит у внедорожников и вездеходов.

Какие виды дифференциалов бывают?

Решением этих проблем является дифференциал повышенного трения (LSD, его ещё называют дифференциалом с ограниченным проскальзыванием). Дифференциалы повышенного трения используют различные механизмы для обеспечения нормального дифференциального действия в различных условиях езды. Когда колесо скользит, такой дифференциал позволяет передать больше крутящего момента как раз на нескользящее колесо.

На внедорожниках и вездеходах также применяются дифференциалы с ручным отключением, которые, впрочем, очень часто не защищены от случайного отключения или отключения не в то время по незнанию — дело в том, что возможность отключения дифференциала на ходу влечёт за собой возможную его поломку, и это распространённая проблема.

Что такое вискомуфта (вязкая муфта)?

Вискомуфта чаще всего встречается во всех полноприводных машинах. И, если Вы читали статью о принципе работы гидротрансформатора, то знайте, что вискомуфта имеет схожую с ним схему работы. Она широко используется для связи задних колёс с передними таким образом, что когда один набор колёс начинает проскальзывать, крутящий момент будет передан на другой набор, тем самым решая злободневную проблему буксующего колеса, описанную выше.

Вязкая муфта имеет два набора пластин внутри герметичного корпуса, который заполнен вязкой жидкостью (несколько более вязкой, чем трансмиссионное масло, к примеру). Один набор пластин соединён с каждым выходным валом. В нормальных условиях оба набора пластин и их порция вязкой жидкости движутся с одной и той же скоростью. Но когда одна ось пытается вращаться быстрее, возможно, потому что она проскальзывает, множество пластин, соответствующих колёсам этой оси, вращаются быстрее, чем другие. Вязкая жидкость, находящаяся между пластинами, пытается догнать более быстрые диски, тем самым ведя за собой к этому и медленные диски. Это передает больший крутящий момент на медленнее вращающиеся колёса, которые как раз и не скользят.

Устройство вискомуфты

Когда автомобиль поворачивает, разница в скорости между колёсами на одной оси не так велика, как тогда, когда одно из колёс попросту проскальзывает. Чем быстрее пластины вращаются относительно друг друга, тем больше крутящего момента приходится на муфту. Муфта не мешает виткам крутиться, потому что величина крутящего момента, передаваемого во время поворота, мала.

Простой эксперимент с яйцом поможет объяснить поведение вискомуфты. Если Вы поставите яйцо на кухонный стол, скорлупа, белок и желток будут неподвижны. Но когда Вы начнёте раскручивать яйцо, скорлупа яйца будет двигаться с более высокой скоростью, чем белок, а белок немного быстрее, ем желток, но желток затем быстро наверстает упущенное. Кстати, чтобы убедиться в этих словах, проведите эксперимент, как только у Вас появится яйцо: раскрутите его достаточно быстро, а затем остановите его, потом просто отпустите яйцо, и оно начнёт снова вращаться (ну, или хотя бы дёрнется в сторону предыдущего вращения).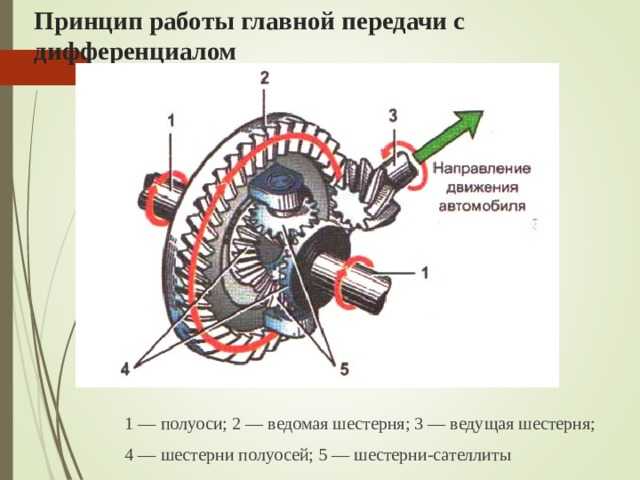  В этом эксперименте мы использовали трение между скорлупой, белком и желтком, применяя силу только на скорлупу. Сначала мы раскрутили фактически скорлупу, и с некоторой задержкой за скорлупой за счёт трения начали раскручиваться белок, а затем и желток. А когда мы остановили скорлупу, то то же трение — между всё еще движущимся желтком, белком и скорлупой — применило силу к скорлупе, заставляя его ускориться. Так и в случае вискомуфты, сила передаётся между жидкостью и наборами пластин таким же образом, как между желтком, белком и скорлупой.

Что такое дифференциал Torsen?

Дифференциал Torsen является чисто механическим устройством: он не завязан никакой электроникой, а также муфтами или вязкими жидкостями и по своей сути представляет собой довольно простой механизм, очень схожий с открытым дифференциалом.

Torsen работает также, как и открытый дифференциал, когда величина крутящего момента между двумя ведущими колёсами равная. Но как только одно из колёс начинает терять сцепление с дорогой, разница в крутящем моменте приводит к блокировке вместе шестерен в дифференциале Torsen.

Такой дифференциал часто используется в мощных и очень мощных полноприводных машинах. Как и вискомуфта, он часто используется для передачи мощности между передними и задними колёсами. И в этом применении дифференциал Torsen превосходит вискомусту, потому что передаёт крутящий момент на колёса стабильно перед тем, как фактически начинается скольжение. Однако, если один набор колёс теряет сцепление с дорогой полностью, то дифференциал Torsen будет не в состоянии перенести крутящий момент на другой набор колёс из-за своей конструкции и принципа работы такого дифференциала.

Так выглядит современный дифференциал Torsen

Кстати, почти все автомобили Hummer используют дифференциал Torsen между передней и задней осями. При этом, руководство пользователя для Hummer предлагает новое решение проблемы, когда одно колесо полностью теряет сцепление с дорогой: нажимайте на педаль тормоза. Применяя тормоз, крутящий момент подаётся на колёса, которые находятся в воздухе, а затем переходят к колёсам, которые смогут вытащить автомобиль из «каши».

Дифференциал. Как работает дифференциал?

 Дифференциал. Как работает дифференциал?

Он есть в каждой машине, и без него невозможно безопасно повернуть – дифференциальный механизм, о котором многие знают, но не многие способны объяснить, как он работает.

Зачем вообще нужен дифференциал?

Дифференциал позволяет колесам, прикрепленным к одной оси, вращаться с разной скоростью. Это используется на каждом повороте, когда внутренние колеса поворачиваются медленнее, чем внешние. Если бы они были жестко соединены друг с другом, внутреннее колесо должно было бы все время скользить, чтобы не отставать от внешнего.

Дифференциал — принцип работы

Дифференциал состоит из набора шестерен, управление которыми в движении может показаться сложным, но на самом деле это не так уж и трудно. На концах карданного вала находятся вышеупомянутые шестерни, которые, когда начинают двигаться, приводят в движение и колеса транспортного средства. Они соединены с зубчатым венцом, который распределяет крутящий момент от двигателя.

Однако это не прямая связь – между шестернями на полуосях и ведущим колесом. На элементе, называемом крестом, размещены дополнительные колеса, так называемые сателлиты. При движении прямо и в условиях хорошего сцепления они двигаются с одинаковой скоростью. Когда вы входите в угол и есть разница в скорости вращения колес транспортного средства, сателлиты также начинают вращаться на рычагах поперечины. Другими словами, часть крутящего момента не попадает в медленно движущееся колесо (то есть внутри дуги), заставляя его проскальзывать и нагружая всю систему, но плавно «используется» дифференциалом.

Дифференциал повышенного трения

Движение без дифференциала было бы невозможно, но его использование также имеет свои недостатки. Дифференциал не заставляет колеса вращаться с одинаковой скоростью, поэтому можно спокойно проходить поворот. Колеса также не вращаются плавно, когда у них разное сцепление с дорогой, что обычно бывает на скользкой поверхности или бездорожье. Если одно колесо теряет сцепление с дорогой (например, на льду), то оно будет вращаться очень быстро, потому что это позволяет дифференциал, в то время как другое колесо с хорошим сцеплением получит гораздо меньший крутящий момент. Когда вы видите, как автомобиль пытается выбраться из грязи, одно колесо которого бесполезно крутится, а другое даже не хочет дергаться, – это работает дифференциал.

При обычном использовании легкового автомобиля это не проблема, но есть автомобили (и водители), для которых это является серьезным неудобством. Например, речь идет о спорткарах, в которых очень важно по максимуму использовать доступное сцепление с дорогой. Для этого используются дифференциалы с повышенным внутренним трением, обычно называемые механизмами повышенного трения.

Фактически, дифференциалы с повышенным внутренним трением могут иметь различную структуру, но все они имеют одну и ту же задачу. Эта задача состоит в том, чтобы создать дополнительное трение в дифференциале, достигнув эффекта, при котором при свободном вращении (например, на льду) восстанавливается тяга так, что больше мощности может передаваться колесу, которое действительно имеет тягу.

В реальном дифференциале с повышенным внутренним трением, например, используются муфты, расположенные у шестерен на полуосях. Когда происходит проскальзывание, муфта начинает создавать дополнительное трение, которое помогает уравновесить мощность, воздействующую на колеса. Производители также все чаще используют так называемый электронный дифференциал, в котором используются элементы системы ABS. Когда система обнаруживает занос одного колеса, она замедляет его с помощью тормозов, в результате чего дифференциал направляет больше мощности на другое колесо.

Блокировка дифференциала

Дифференциальная передача также зависит от рельефа местности по причинам, указанным выше. Вот почему настоящие внедорожники используют его полную блокаду. Это означает, что колеса жестко связаны друг с другом и всегда вращаются с одинаковой скоростью. В некоторых автомобилях вы также можете найти центральную блокировку дифференциала, которая уравновешивает мощность, передаваемую на переднюю и заднюю оси.

Таким образом, автомобиль только с одним колесом, имеющим тягу, может продолжать движение, поскольку к нему может быть приложен достаточный крутящий момент, чтобы заставить транспортное средство двигаться. Это можно использовать только на скользком грунте, где колеса могут свободно катиться. В противном случае может быть поврежден дифференциал, который при блокировке заставит колеса вращаться с такой же скоростью, как если бы автомобиль был без него.

Дифференциально-алгебраические уравнения — Scholarpedia

Постпубликационная деятельность

Куратор: Ву Хоанг Линь

Авторы:

0. 36 —

Евгений Михайлович Ижикевич

0,18 —

Ник Орбек

0,18 —

Барбара Зубик-Коваль

0,18 —

Линда Р. Петцольд

0,09 —

Мишель Л. Джонс

0,09 —

Бенджамин Броннер

0,09 —

Стивен Л. Кэмпбелл

• Доктор Стивен Л. Кэмпбелл, Государственный университет Северной Каролины, Роли, Северная Каролина, США.

• Ву Хоанг Линь, Факультет математики, механики и информатики Вьетнамского национального университета, Ханой, Вьетнам

• Линда Р. Петцольд, факультет машиностроения и факультет компьютерных наук, Калифорнийский университет в Санта-Барбаре, Калифорния

Дифференциально-алгебраическое уравнение ( DAE ) представляет собой уравнение, содержащее неизвестную функцию и ее производные.
ДАУ (первого порядка) в наиболее общем виде имеет вид
\[\тег{1}
F(t,x,x’)=0,\quad t_0\leq t\leq t_f,
\]

где \(x=x(t)\,\) неизвестная функция и \(F=F(t,u,v)\) имеют \(N\) компонентов, обозначаемых \(x_i\) и \(F_i,\i=1,2,…,N\ ,\) соответственно. Каждая ДАУ может быть записана как ДАУ первого порядка. Термин DAE обычно зарезервирован для случая, когда старшая производная \(x’\) не может быть решена в терминах других терминов \(t, x,\), когда (1) рассматривается как алгебраическая связь между тремя переменными \(t, x, x’\ .\) Якобиан \(\partial F/\partial v\) вдоль частного решения ДАУ может быть сингулярным. Системы уравнений типа (1) также называются неявными системами, обобщенными системами или системами дескрипторов. ДАУ может быть задачей с начальным значением, где \(x\) задано в начальный момент времени, \(x(t_0)=x_0\,\), или задачей с граничным значением, где решение зависит от \(N\) двухточечные граничные условия \(g(x(t_0),x(t_f))=0\ .\)

Метод решения ДАУ будет зависеть от его структуры.
Особым, но важным классом ДАУ вида (1) являются полуявные ДАУ или обыкновенные дифференциальные уравнения (ОДУ) с ограничениями
\[\тег{2}
\begin{массив}{ccc}
у’ & = & f(t,y,z) \\
0 & = & g(t,y,z),
\конец{массив}
\]

, которые часто появляются в приложениях. Здесь \(x=(y,z)\) и \(g(t,y,z)=0\) — явные ограничения.

Где возникают DAE?

ДАУ в общей форме (1) или в специальной форме (2) возникают при математическом моделировании широкого спектра технических и научных задач. 2& = &1.
\конец{массив}
\]

В этом очень простом случае механической системы из нескольких тел замена переменных \(x_1=\sin \theta, x_2=\cos \theta \)
а затем некоторые алгебраические действия дают хорошо известное ОДУ для маятника \(\theta»=-g \sin \theta\ .\) Однако такая простая процедура исключения обычно невозможна в более общих ситуациях.

Дополнительные примеры реальных систем DAE, включая многотельные механические системы, электрическую схему и заданную задачу управления траекторией, можно найти в Brenan et al. (1996). Следует отметить, что ограничение в механике, т.е. в примере с маятником является физическим, в то время как ограничение в других задачах, таких как задача о заданном пути, не является физическим, а скорее является частью технических характеристик.

Почему они важны?

ДАУ являются обобщением обыкновенных дифференциальных уравнений (ОДУ)
\[\тег{5}
\begin{массив}{ccc}
х’&=&f(t,x),
\конец{массив}
\]

, для которого существует очень богатая литература как по математической теории, так и по численному решению. В то время как ОДУ стандартной формы может быть записано как ДАУ, более общая форма ДАУ допускает проблемы, которые могут сильно отличаться от ОДУ стандартной формы. К классу ДАУ относятся задачи, обладающие фундаментальными математическими свойствами, отличными от свойств ОДУ, а также создающие дополнительные трудности при их численном решении. С другой стороны, неявный DAE
модели формулируются более естественным образом, чем явные, как показывают приведенные выше примеры. Легче получить сложную модель DAE, поэтому крайне желательно иметь возможность работать с моделью DAE, если это возможно.
9′ & = & г \\
0 & = & у — q(t),
\конец{массив}
\]

где задана достаточно гладкая функция \(q\). Ясно, что единственным решением является \(y=q(t),\z=q'(t)\ ,\), и никаких начальных или граничных условий не требуется. То есть, если наложено произвольное начальное условие, оно вполне может быть несовместимо с ДАУ. Кроме того, видно, что решение зависит от производной неоднородной части (или производной входа, если роль входа играет функция \(q\)), чего не может быть в случае ОДУ. Другое отличие состоит в том, что даже если даны непротиворечивые начальные значения, теория существования и единственности более сложна и включает дополнительные технические предположения, помимо достаточной гладкости, как в случае ОДУ. Тот факт, что в первом уравнении этого примера необходимо дифференцировать \(y\ ,\), что влечет за собой дифференцирование входной функции \(q\ ,\), чтобы найти \(z\ ,\), делает ключевым разница. Для ОДУ стандартной формы решение всегда более непрерывно, чем вход. Другими словами, DAE может включать как интеграцию, так и дифференциацию.

Индекс и математическая структура

Индекс

Индекс — это понятие, используемое в теории ДАУ для измерения расстояния от ДАУ до связанного с ним ОДУ. Индекс представляет собой неотрицательное целое число, которое предоставляет полезную информацию о математической структуре и потенциальных сложностях при анализе и численном решении ДАУ. В общем случае, чем выше индекс ДАУ, тем больше трудностей можно ожидать при его численном решении. Существуют различные определения индекса: индекс Кронекера (для ДАУ с линейным постоянным коэффициентом), индекс дифференцирования (Бренан и др. 19).96), индекс возмущения (Хайрер и др., 1996), индекс управляемости (Грипентрог и др., 1986), геометрический индекс (Рабье и др., 2002) и индекс странности (Кункель и др., 2006). На простых задачах они идентичны. На более сложных нелинейных и полностью неявных системах они могут быть другими. Фактически индекс может стать локальным понятием с разными значениями в разных регионах. Индекс может быть даже не определен в так называемых особых точках, которые обычно демонстрируют явление тупика (Rabier et al. 2002, Riaza 2008).

Поскольку ДАУ включает в себя смесь дифференцирований и интегрирований, можно надеяться, что дифференцирование ограничений (в полуявной системе ДАУ) и подстановка по мере необходимости из дифференциальных уравнений, при необходимости многократно, даст явную систему ОДУ для всех неизвестные. Решения ДАУ — это те решения этого ОДУ, которые находятся в подмножестве, называемом многообразием решений. Количество повторений, необходимых для этого преобразования, называется дифференциальным индексом ДАУ. Таким образом, ОДУ имеют индекс \(0\ .\) Рассмотрим несколько простых примеров.

Пример. Пусть \(q(t)\) — заданная гладкая функция, и рассмотрим следующие задачи для \(x(t)\ .\)

• Скалярное уравнение

\[\тег{7}
х (т) = д (т)
\]

является (тривиальным) ДАУ с индексом 1, поскольку для получения ОДУ \(x’=q'(t) \ .\) требуется одно дифференцирование

• Для системы

\[\тег{8}
\begin{массив}{ccc}
x_1& = & q(t) \\
х_2 & = & х_1′,
\конец{массив}
\]

первое уравнение дифференцируется, чтобы получить \(x_2=x_1’=q'(t) \), а затем \(x_2’=x_1»=q»(t) \ .\) Индекс равен \(2 \), так как необходимы два дифференцирования.

Обратите внимание, что хотя \(m\) начальные или граничные условия должны быть заданы для определения решения ОДУ первого порядка размера \(m\ ,\) для простых ДАУ в приведенном выше примере, решение полностью определяется правая часть и имеется только одно согласованное начальное условие. Общие системы DAE обычно включают также некоторые подсистемы ODE. Таким образом, система ДАУ в общем случае будет иметь \(l\) степеней свободы , где \(l\) находится где-то между \(0\) и \(m\ .\). , или, по крайней мере, не очевидно, чтобы определить, какие \(l\) фрагментов информации необходимы для определения решения. Начальное или граничное условие, заданное для ДАУ, должно быть непротиворечивым. Другими словами, они должны удовлетворять ограничениям и, возможно, даже дифференцированным ограничениям системы. Например, начальное условие для системы индекса 1 (7) (которое необходимо, если записать его как ОДУ) должно удовлетворять \(x_1(0)=q(0)\ .\) Для системы индекса 2 (8) ситуация несколько сложнее. Любое решение должно удовлетворять не только очевидному ограничению \(x_1(t)=q(t)\,\), но и скрытому ограничению \(x_2(t)=q'(t)\,\), поэтому единственное согласованное начальные условия: \(x_1(0)=q(0),\x_2(0)=q'(0)\ .\) Это важное различие между index-1 и более высокий индекс (индекс больше \(1\)) DAE. DAE с более высоким индексом включают в себя некоторые скрытые ограничения.

Снова рассмотрим полуявный ДАУ (2). Индекс равен единице, если \(\partial g/\partial z\) невырожденно, потому что в этом случае одно дифференцирование алгебраического уравнения дает \(z’\ .\). Для полуявного индекса-1 ДАУ можно различить между дифференциальными переменными \(y\), производная которых фигурирует в уравнениях, и алгебраическими переменными \(z\), производная которых явно не фигурирует. Также стоит отметить, что алгебраические переменные могут быть менее гладкими, чем дифференциальные переменные на одну производную, например. алгебраические переменные могут быть недифференцируемыми.

В общем случае (1) каждая компонента решения \(x\) может быть смесью дифференциальных и алгебраических компонент, что значительно усложняет качественный анализ, а также численное решение таких высокоиндексных задач и более рискованно. В этом смысле полуявная форма развязана. Любой ДАУ (1) можно записать в полуявном виде, введя новую переменную \(z=x’\ . \) Однако индекс нового ДАУ увеличивается на единицу. Наконец, важно отметить, как показывает следующий пример, что в общем случае индекс может зависеть и от конкретного решения, а не только от вида ДАУ.
9Т\)
\[\тег{9}
\begin{массив}{rcl}
х_1’& = & х_3 \\
0 & = & x_2(1-x_2)\\
0 & = & x_1x_2+x_3(1-x_2)-t.
\конец{массив}
\]

Второе уравнение имеет два решения \(x_2=0\) и \(x_2=1\ .\) Если задана непрерывность \(x_2\), то \(x_2\) не переключается между этими двумя значениями . Легко видеть, что если \(x_2=0\ ,\), то система находится в полуявном виде и имеет индекс-1, а для случая \(x_2=1\ ,\) система имеет индекс-2 и, в отличие от случая с индексом 1, начальное значение \(x_1\) не требуется.

Теперь, если заменить алгебраическое уравнение с \(x_2\) на \(x_2’=0\ ,\), то индекс новой системы ДАУ будет зависеть от начального условия. Если \(x_2(0)=1\) индекс равен 2, иначе индекс равен 1.

Специальные формы ДАУ

Общая система ДАУ (1) может включать в себя задачи, которые не являются четко определенными в математическом смысле, а также задачи, которые приведут к отказу любого метода прямой дискретизации (см. раздел «Численное решение»). К счастью, многие проблемы с более высоким индексом, встречающиеся на практике, могут быть выражены как комбинация более ограничительных структур ОДУ в сочетании с ограничениями.
Одним из наиболее важных классов систем являются 9{\ простое число} & = & е (т, у, г) \\
0 & = & g(t,y,z),
\конец{массив}
\]

где якобиан \(g_z\) считается неособым для всех t. Это всего лишь полуявная система DAE с индексом 1, упомянутая выше. Полуявные ДАУ с индексом 1 очень тесно связаны с неявными ОДУ. После решения для \(z\) в алгебраическом уравнении (используя теорему о неявной функции, это в принципе можно сделать), подстановка \(z\) в дифференциальное уравнение дает так называемое основное ОДУ в \(y\) (хотя уникальность не гарантируется). Однако по разным причинам эта процедура не всегда рекомендуется на практике для численного решения.
9{\ простое число} & = & е (т, у, г) \\
0&=&g(t,y),
\конец{массив}
\]

где \(g_y f_z\) предполагается невырожденным для всех t. Обратите внимание, что во втором уравнении отсутствует алгебраическая переменная \(z\). Это чистый ДАУ индекса 2, и все алгебраические переменные играют роль переменных индекса 2.
Пример, возникающий при моделировании потока несжимаемой жидкости с помощью дискретизированных уравнений Навье-Стокса, приведен в Ascher et al. (1998).

Численное решение

Численные подходы к решению ДАУ можно разделить примерно на два класса: (i) прямая дискретизация данной системы и (ii) методы, которые включают переформулировку (например, уменьшение индекса) в сочетании с дискретизацией. Стремление к как можно более прямой дискретизации возникает из-за того, что переформулировка может быть дорогостоящей, может потребовать большего ввода данных от пользователя и большего вмешательства пользователя. Причина популярности подходов с переформулировкой заключается в том, что, как оказалось, прямая дискретизация ограничена в своей полезности в основном системами Hessenberg DAE с индексом 1, индексом 2 и индексом Hessenberg 3.

К счастью, многие ДАУ, встречающиеся в практических приложениях, имеют либо индекс 1, либо, если индекс выше, могут быть выражены в виде простой комбинации систем Хессенберга. Однако могут возникнуть некоторые трудности в худшем случае, и самые надежные прямые приложения численных методов ОДУ не всегда работают так, как можно было бы надеяться, даже для этих ограниченных классов задач. Для DAE с индексом больше двух обычно лучше всего использовать один из методов уменьшения индекса для решения проблемы в форме с более низким индексом.

Дифференциальные уравнения, такие как
\[\тег{12}
\begin{массив}{rcl}
у’ & = & f(t,y,z) \\
\varepsilon z’& = & g(t,y,z),
\конец{массив}
\]

, где \(\varepsilon\) — малый параметр, называются сингулярно возмущенными системами ОДУ. Когда для параметра \(\varepsilon\) установлено значение \(0\ ,\), (12) становится DAE (2). Поскольку система (12) является (вообще) очень жесткой при малых \(\varepsilon\ ,\), естественно рассмотреть методы для жестких ОДУ прямой дискретизации предельного ДАУ, а для ДАУ вида (1) в общем. В частности, полезны методы ОДУ с жестким затуханием, такие как методы коллокации BDF и Радау.

Численные методы/Прямая дискретизация

• Обратный метод Эйлера/Пример неустойчивости

Идея прямой дискретизации проста: аппроксимировать \(x\) и \(x’\) формулой дискретизации, подобной многошаговым методам или методам Рунге-Кутты. В качестве иллюстрации использования прямой дискретизации рассмотрим обратный метод Эйлера, простейший метод, обладающий свойством жесткого затухания. Применение формулы обратной разности к \(x’\) в (1), система \(N\) нелинейных уравнений для \(x_n\)
\[\тег{13}
F(t_n,x_n,\frac{x_n-x_{n-1}}{h_n})=0 \mbox{ для } n=1,2,…,
\]

результатов. Здесь \(t_n\) — моменты времени, когда мы вычисляем приближение, \(x_n\) — приближение \(x(t_n)\,\) и \(h_n=t_n-t_{n-1}\ ) — временной шаг или размер шага. После рекурсивного решения этой нелинейной системы уравнений получается численное решение уравнения (1). Этот метод хорошо работает для ДАУ с индексом 1 и особенно подходит для жестких ДАУ с индексом 1, а также для жестких ОДУ.

Для ДАУ с более высоким индексом этот простой метод, как и другие методы,
не всегда работает. В худшем случае существуют простые системы ДАУ с более высоким индексом с четко определенными и устойчивыми решениями, для которых обратный метод Эйлера, а фактически все другие многошаговые методы и методы Рунге-Кутты неустойчивы или даже неприменимы. См. пример 10.1 в Ascher et al. (1998). См. также моделирование механики нескольких тел, где визуализируется использование стабильных и нестабильных численных методов. Некоторые практические трудности могут возникнуть и при решении нелинейной системы (13) для \(x_n\) при заданном \(x_{n-1}\ .\). метод. Эти технические трудности объясняют, почему, как правило, прямая дискретизация полностью неявных ДАУ с индексом выше единицы не рекомендуется. Для полностью неявных ДАУ индекса-1 и полуявного индекса-2 было показано, что обратный метод Эйлера является точным, устойчивым и сходящимся первого порядка. Подробные обсуждения и результаты сходимости можно найти в Brenan et al. s a_{ij}K_j,\quad i=1,2,…,s,
\конец{массив}
\]
9s a_{ij}K_j,\\
g\left(t_{n-1}+c_i h,Y_{ni},Z_{ni}\right)&=&0. \quad i=1,2,…,s.
\конец{массив}
\]

Можно избежать квадратурного шага (16) для алгебраических переменных \(z\), используя жестко точные методы, т. е. методы Рунге-Кутты, удовлетворяющие \(b_j=a_{sj},\ j=1 ,2,…,s,\ .\) Вместо (16) просто задается \(y_n=Y_{ns}\ .\) Как и в случае общих многошаговых методов, имеются дополнительные условия порядка, коэффициенты метода должны удовлетворять требованиям, чтобы метод достиг порядка выше 2. Для методов Рунге-Кутты требование дополнительных условий порядка возникает даже для полуявных ДАУ с индексом 1.

Следует также отметить, что реализация методов прямой дискретизации для ДАУ сталкивается с некоторыми дополнительными практическими трудностями, такими как получение согласованного набора начальных условий, обработка плохой обусловленности итерационной матрицы и, наконец, оценка ошибок и управление ступенчатым размером для ДАУ Hessenberg с индексом 2.

Для некоторых специальных классов ДАУ, таких как полуявные ДАУ в форме Хессенберга и ОДУ на многообразиях, в частности для ДАУ, возникающих в механике множественных тел, существуют очень эффективные и надежные численные методы, называемые стабилизированными или проекционными методами. Основная идея состоит в том, чтобы сначала дискретизировать дифференциальные уравнения с помощью соответствующего численного метода ОДУ. За этим шагом следует этап постстабилизации или проекции координат, чтобы приблизить численное решение к удовлетворению ограничения, см. Eich-Soellner et al. (1998).

Для получения более подробной информации о числовых значениях DAE см. Ascher et al. (1998), Бренан и др. (1996) и Хайрер и соавт. (1998).

Программное обеспечение

Проблемы с начальными значениями

• Код DASSL от Petzold использует формулы BDF для решения ДАУ общего индекса 1, см. Brenan et al. (1996) для деталей. Также доступны версии для крупномасштабных задач (называемые DASPK) и для анализа чувствительности. Некоторые более поздние версии DASPK также могут решать DAE с индексом Hessenberg 2. Существует также код DASPKADJOINT, который реализует сопряженный метод для анализа чувствительности систем DAE.

• Код RADAU5 от Hairer & Wanner (1998) основан на трехэтапном методе коллокации Радау. Он решает ДАУ вида \(Mx’=f(t,x)\,\), где \(M\) — постоянная квадратная матрица, которая может быть сингулярной. Кодекс применим к задачам индекса 1,2,3. Переменные с более высоким индексом должны быть идентифицированы пользователем.

• Код IDA является частью программного пакета SUNDALS (SUite of Nonlinear and DIfferential/ALgebraic Solutions), который был разработан Сербаном и Хиндмаршем в Ливерморской национальной лаборатории им. Лоуренса, США. Он написан на C для решения нелинейных ДАУ, но получен из пакета DASPK, написанного на Фортране. Также доступен связанный с СОЛНЕЧНЫМИ ЧАСАМИ код CPODES (решатель координатной проекции для ОДУ с инвариантами), написанный Сербаном.

• DAEPACK — это программная библиотека, разработанная Полом И. Бартоном и его группой в Массачусетском технологическом институте. DAEPACK — это аббревиатура от «Пакет дифференциально-алгебраических уравнений», однако его область применения не ограничивается анализом ДАУ. DAEPACK включает в себя как символьные, так и числовые компоненты для моделирования, а также для общих числовых расчетов.

• Другие коды: MEXX by Lubich et al. (1992), LIMEX Deuflhard et al. (1987), GELDA и GENDA Kunkel et al. (1997) также доступны.

Краевые задачи

• Код COLDAE по Ascher et al. (1994) использует спроецированное сопоставление Гаусса с BVP для полуявного индекса 2 DAE.

Каталожные номера

• Ascher U.M.; Петцольд Л.Р. (1998) Компьютерные методы решения обыкновенных дифференциальных уравнений и дифференциально-алгебраических уравнений. Общество промышленной и прикладной математики (SIAM), Филадельфия, Пенсильвания.
• Бренан К.Е.; Кэмпбелл С.Л.; Петцольд Л.Р. (1996) Численное решение начальных задач в дифференциально-алгебраических уравнениях. Пересмотренное и исправленное переиздание оригинала 1989 г. с дополнительной главой и дополнительными ссылками. Классика прикладной математики, 14. Общество промышленной и прикладной математики (SIAM), Филадельфия, Пенсильвания.
• Кэмпбелл С.Л. и Петцольд Л.Р. (1983) Канонические формы и разрешимые сингулярные системы дифференциальных уравнений, SIAM J. Alg. Диск. Мет. 4:517-521
• Хайрер Э.; Ваннер Г. (1996) Решение обыкновенных дифференциальных уравнений. II. Жесткие и дифференциально-алгебраические задачи. Второе издание. Серия Springer по вычислительной математике, 14. Springer-Verlag, Берлин.
• Петцольд Л.Р. (1982) Дифференциальные/алгебраические уравнения не являются ОДУ, SIAM J. Sci. Стат. Вычисл., 3:367-384
• Рабье П.Дж.; Рейнбольдт В.К. (2002) Теоретический и численный анализ дифференциально-алгебраических уравнений. Справочник по численному анализу, Vol. VIII, 183–540, Handb. Число. Anal., VIII, Северная Голландия, Амстердам.
• Риаза Р. (2008), Дифференциально-алгебраические системы: аналитические аспекты и применение схем, World Scientific, Сингапур.

Внутренние ссылки

• Джон Батчер (2007) Методы Рунге-Кутты. Академия, 2(9):3147
• Билл Гир (2007) Формулы обратного дифференцирования. Академия, 2(8):3162
• Ян Гладуэлл (2008) Краевая задача. Академия, 3(1):2853
• Алан С. Хиндмарш и Раду Сербан (2007) Решатели уравнений для солнечных часов. Академия, 2(3):2860
• Здислав Яцкевич (2007) Общие линейные методы. Академия, 2(4):2852
• Лоуренс Ф. Шампайн и Скип Томпсон (2007) Проблемы с начальными значениями. Академия, 2(3):2861
• Лоуренс Ф. Шампайн и Скип Томпсон (2007) Жесткие системы. Академия, 2(3):2855

Внутренние ссылки

• Билл Гир (2007) Формулы обратного дифференцирования. Scholarpedia, 2(8):3162.

• Ян Гладуэлл (2008) Краевая задача. Scholarpedia, 3(1):2853.

• Джеймс Мейсс (2007) Динамические системы. Scholarpedia, 2 (2): 1629.

• Здислав Яцкевич (2007) Общие линейные методы. Scholarpedia, 2(4):2852.

• Лоуренс Ф. Шампайн и Скип Томпсон (2007) Проблемы с начальными значениями. Scholarpedia, 2(3):2861.

• Кендалл Э. Аткинсон (2007) Численный анализ. Scholarpedia, 2(8):3163.

• Джон Батчер (2007) Методы Рунге-Кутты. Академия, 2(9)):3147.

• Филип Холмс и Эрик Т. Ши-Браун (2006) Стабильность. Scholarpedia, 1 (10): 1838.

• Никола Гульельми и Эрнст Хайрер (2007) Жесткие уравнения с запаздыванием. Scholarpedia, 2(11):2850.

• Лоуренс Ф. Шампайн и Скип Томпсон (2007) Жесткие системы. Scholarpedia, 2(3):2855.

• Алан С. Хиндмарш и Раду Сербан (2007) Решатели уравнений для солнечных часов. Scholarpedia, 2(3):2860.

Рекомендуемое чтение

• Эйх-Зёлльнер Э. и Фюрер К. (1998) Численные методы в многотельных системах. Teubner Verlag, Штутгарт, Германия.
• Грипентрог Э., Марц Р. (1986) Дифференциально-алгебраические уравнения и их числовая обработка. С немецким, французским и русским резюме. Teubner-Texte zur Mathematik [Тексты Тойбнера по математике], 88. BSB BG Teubner Verlagsgesellschaft, Лейпциг.
• Хайрер Э., Любич К. и Рош М. (1989) Численное решение дифференциально-алгебраических систем методами Рунге-Кутты, конспект лекций по математике № 1409, Springer-Verlag, Берлин.
• Кункель П., Мерманн В. (2006), Анализ дифференциально-алгебраических уравнений и численное решение. Издательство EMS, Цюрих, Швейцария.
• Рабье П.Дж.; Рейнбольдт В.К. (2002) Теоретический и численный анализ дифференциально-алгебраических уравнений. Справочник по численному анализу, Vol. VIII, 183–540, Handb. Число. Anal., VIII, Северная Голландия, Амстердам.
• Риаза Р. (2008), Дифференциально-алгебраические системы: аналитические аспекты и применение схем, World Scientific, Сингапур.

Внешние ссылки

• Веб-сайт Линды Петцольд
• Веб-сайт Стивена Л. Кэмпбелла
• Веб-сайт Ву Хоанг Линя

См. также

Динамические системы, численный анализ, устойчивость, жесткие уравнения с запаздыванием

Дифференциал функции

Определение дифференциала функции

Рассмотрим функцию y = f ( x ), которая непрерывна на интервале [ а , б ]. Предположим, что в какой-то момент x ₀ ∈ [ a , b ] независимая переменная увеличивается на Δ x . Приращение функции Δ y , соответствующее изменению независимой переменной Δ x , равно

\[\Delta y = \Delta f\left( {{x_0}} \right) = f\left( {{x_0} + \Delta x} \right) — f\left( {{x_0}} \right ).\]

Для любой дифференцируемой функции приращение Δ y можно представить в виде суммы двух слагаемых:

\[\Delta y = A\Delta x + \omicron\left( {\Delta x} \right),\]

, где первый член (называемый главной частью приращения) линейно зависит от приращения \(\Delta x,\), а второй член имеет более высокий порядок малости по отношению к \(\Delta x. \) выражение \(A\Delta x\) называется дифференциалом функции и обозначается \(dy\) или \(df\left( {{x_0}} \right).\)

Рассмотрим идею разделения приращения функции \(\Delta y\) на две части на следующем простом примере. Дан квадрат со стороной \({x_0} = 1 \,\text{m}\,\) (рис. \(1\)). 92.\)

Обратите внимание, что в этом примере коэффициент \(A\) равен значению производной от \(S\) в точке \({x_0}:\)

\[А = 2{х_0}.\]

Оказывается, для любой дифференцируемой функции справедлива следующая теорема:

Коэффициент \(A\) при главной части приращения функции в точке \({x_0}\) равен значению производной \(f’\left( {{x_0}} \right )\) в этот момент, то есть приращение \(\Delta y\) равно

\[\Delta y = A\Delta x + \omicron\left( {\Delta x} \right) = f’\left({{x_0}} \right)\Delta x + \omicron\left( {\ Дельта х} \справа).\]

Деление обеих частей уравнения на \(\Delta x \ne 0\) дает

\[\frac{{\Delta y}}{{\Delta x}} = A + \frac{{\omicron\left({\Delta x} \right)}}{{\Delta x}} = f ‘\left( {{x_0}} \right) + \frac{{\omicron\left( {\Delta x} \right)}}{{\Delta x}}. \]

В пределе при \(\Delta x \to 0\) мы получаем значение производной в точке \({x_0}:\)

\[y’\left( {{x_0}} \right) = \lim\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} = A = f’ \влево( {{x_0}} \вправо).\]

Здесь мы учли, что для малой величины \(\omicron\left( {\Delta x} \right)\) более высокого порядка малости, чем \(\Delta x,\) предел равен

\[\lim\limits_{\Delta x \to 0} \frac{{\omicron\left( {\Delta x} \right)}}{{\Delta x}} = 0.\]

Предполагая, что дифференциал независимой переменной \(dx\) равен ее приращению \(\Delta x:\)

\[дх = \Дельта х,\]

получаем из отношения

\[dy = A\Delta x = y’dx\]

то

\[y’ = \frac{{dy}}{{dx}},\]

, поэтому производную функции можно представить как отношение двух дифференциалов.

Геометрический смысл дифференциала функции

На рис. \(2\) схематично показано разбиение приращения \(\Delta y\) на главную часть \(A\Delta x\) (дифференциал функции) и член более высокого порядка малости \(\ омикрон\влево( {\Delta x} \вправо). \)

Рис. 2.

Касательная \(MN\), проведенная к кривой функции \(y = f\left( x \right)\) в точке \(M,\), как известно, имеет угол наклона \(\alpha,\) тангенс которой равен производной:

\[\tan \alpha = f’\left( {{x_0}} \right).\]

Когда независимая переменная изменяется на \(\Delta x\), тангенс увеличивается на \(A\Delta x.\) Это линейное приращение, образованное тангенсом, является просто дифференциалом функции. Оставшаяся часть полного приращения \(\Delta y\) (отрезок \(N{M_1}\)) соответствует «нелинейной» добавке более высокого порядка малости по \(\Delta x.\)

Свойства дифференциала

Пусть \(и\) и \(v\) — функции переменной \(х\). Дифференциал имеет следующие свойства:

1. Постоянная может быть вынесена за знак дифференциала:

   \[d\влево( {Cu} \вправо) = Cdu,\]

   где \(С\) — постоянное число.

2. Дифференциал суммы (разности) двух функций равен сумме (разности) их дифференциалов:

   \[d\left( {u \pm v} \right) = du \pm dv. \]

3. Дифференциал константы равен нулю:

   \[d\влево(С\вправо) = 0.\]

4. Дифференциал независимой переменной \(x\) равен ее приращению:

   \[dx = \Дельта x.\]

5. Дифференциал линейной функции равен ее приращению:

   \[d\left( {ax + b} \right) = \Delta \left( {ax + b} \right) = a\Delta x.\]

6. Дифференциал произведения двух функций:

   \[d\left( {uv} \right) = du \cdot v + u \cdot dv.\] 9{n — 1}}dx,\;\;\;d\left( {\ln x} \right) = \frac{{dx}}{x},\;\;\;d\left( {\ sin x} \right) = \cos x dx,\]

   и так далее.

   Формоинвариантность дифференциала

   Рассмотрим композицию двух функций \(y = f\left( u \right)\) и \(u = g\left( x \right).\). Его производную можно найти по цепному правилу:

   \[{y’_x} = {y’_u} \cdot {u’_x},\]

   , где субиндекс обозначает переменную дифференцирования.

   Дифференциал «внешней» функции \(y = f\left( u \right)\) можно записать как

   \[dy = {y’_u}\,du. \]

   Дифференциал «внутренней» функции \(u = g\left( x \right)\) можно представить аналогичным образом:

   \[du = {u’_x}\,dx.\]

   Если в последнюю формулу подставить \(du\), то получится

   \[dy = {y’_u}\,du = {y’_u}{u’_x}\,dx.\]

   Поскольку \({y’_x} = {y’_u} \cdot {u’_x},\), то

   \[dy = {y’_x}\,dx.\]

   Видно, что в случае сложной функции мы получаем выражение для дифференциала в том же виде, что и для «простой» функции. Это свойство называется формоинвариантностью дифференциала.

   Решенные проблемы

   Щелкните или коснитесь проблемы, чтобы увидеть решение.

   Пример 1

   Найдите дифференциал функции \[y = \sin x — x\cos x.\]

   Пример 2

   Найдите дифференциал функции \[y = \cot {\frac{{\ pi x}}{4}}\] в точке \(x = 1.\) 9\prime}} \right) = \cos x — \left( {\cos x + x\left( { — \sin x} \right)} \right) = \cancel{\cos x} — \cancel{\ cos x} + x\sin x = x\sin x.\]

   Дифференциал имеет следующий вид:

   \[dy = y’dx = x\sin x\,dx.