Содержание
Для чего был изобретен интеграл и дифференциал, какое математическое действие лежит в их основе и их значение для естественных и технических наук?
Популярное
Сообщества
ФизикаМатематикаНаука
Max Kravchenko
·
65,9 K
ОтветитьУточнить
Andronick Arutyunov
Математика
916
к.ф.м.н., преподаватель Свободного Университета, доцент МФТИ, с.н.с. Института Проблем… · 11 мая
Одной из первых больших и сложных задач, которые оказалось невозможно решить без нового аппарата была задача о брахистохроне, которую можно сформулировать так: как формы должна быть ледяная горка, чтобы по ней материальная точка скатывалась за минимально время. Удивительно, но решением оказывается не что-то ожидаемое типа дуги окружности или прямой, а дуга циклоиды.
Саму задачу поставил один из представителей славного семейства Бернулли. Ну а решали её помимо его знаменитых родственников также Лопиталь, Лейбниц и Ньютон. Можно сказать, что именно из их работ дифференциальное и интегральное исчисление и родилось в современном виде.
Почитать об этом можно например в статье В.М. Тихомирова, а более подробное и просто изложение, доступное школьникам, в его же книжке «Рассказы о максимумах и минимумах».
Математика, политика, высшая школа и хейт спич
Перейти на t.me/forodirchNEWS
Леонид Коганов
12 мая
Решил подписаться навстречу. Ранее после обдумывания подписался на Сажневу из МК с псевдонимом «Не всё равно»… Читать дальше
Комментировать ответ…Комментировать…
Максим Плеханов
535
Химик, Сотрудник института РАН · 18 янв 2016
Давайте начнем с дифференциала, а точнее с производной, потому что о ней речь заходит у всех еще в школе. Из школьного определения мы знаем «Производная это отношение приращения функции к приращению аргумента». Проще говоря это отношение изменения функции к изменению аргумента, но эта фраза тоже может быть понятна не всем. Функция это некая величина, которая меняется в… Читать далее
Из школьного определения мы знаем «Производная это отношение приращения функции к приращению аргумента». Проще говоря это отношение изменения функции к изменению аргумента, но эта фраза тоже может быть понятна не всем. Функция это некая величина, которая меняется в… Читать далее
1 эксперт согласен
Григорий Смирнов-Пинчуков
25 января 2016
Только вот дифференциал функции это не ее «бесконечно малое изменение», а линейная по аргументам часть ее… Читать дальше
Комментировать ответ…Комментировать…
Леонид Коганов
181
Член ММО — Московского математического Общества. Кстати, старейшего в мире.
Л.М. Коганов. · 11 мая
Классический инфинитезимальный анализ (= исчисление бесконечно малых — усл. = дифференциальное и интегральное (ед.ч.! — Л.К.) исчисление) есть естественная надстройка над элементарной школьной алгеброй.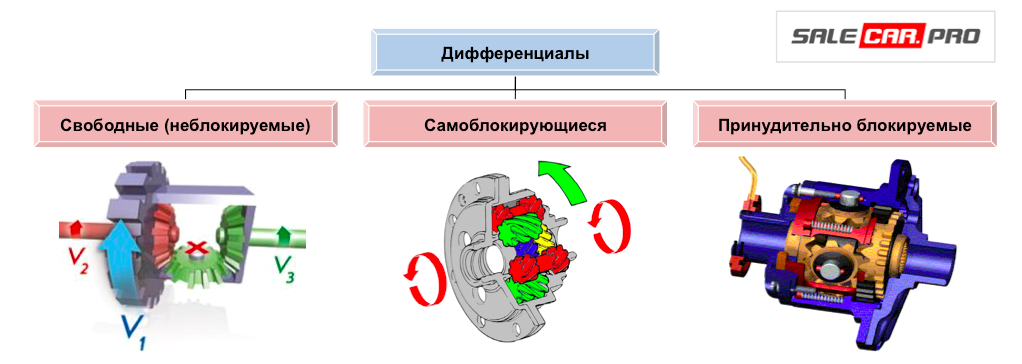 Требующая введения операции предельного перехода и анализа понятия действительного числа.
Требующая введения операции предельного перехода и анализа понятия действительного числа.
Создавался для измерения величин в геометрии и физике, начиная с греческой… Читать далее
Леонид Коганов
22 мая
Продолжим заметки на полях. Полный дифференциал функции, условно двух независимых переменных, в точке (крепления… Читать дальше
Комментировать ответ…Комментировать…
Тёма Ти
1,4 K
Занимаюсь разработкой игр.
Веду активный образ жизни, связанный с акробатикой и танцами.
М… · 22 янв 2016
Добавлю к вышесказанному.
Давайте попробуем определить скорость объекта, который движется из пункта А в пункт Б, между которыми расстояние 100 метров.
Для примера возьмем, что объект прошел это расстояние за 10 сек. Следовательно, средняя скорость равно 100 / 10 = 10 м/с
Но ведь объект мог двигаться не с постоянной скорость, а следующим образом:
Первые 50 метров объект. .. Читать далее
.. Читать далее
Светлана
29 июля 2021
Какое замечательное объяснение! Спасибо!!!
Комментировать ответ…Комментировать…
Irina Georgievskaya
52
Физик, художник, счастливый человек · 19 янв 2016
Производная показывает скорость изменения функции. Самый элементарный пример — это расстояние, скорость, ускорение. Если мы движемся с постоянной скоростью, 5 м/с, то в первую секунду мы будем находиться на расстоянии 5 м от начала, во вторую 10 м от начала и т.д., а производная от нашего места положения — это и есть скорость 5 м/с. Если же у нас неравномерное (равнопере… Читать далее
Комментировать ответ…Комментировать…
Ruslan Y
309
Инженер электронной техники, программист. · 14 мая
Производная это скорость мгновенная df/dt — точка в пространстве времени. Вы же смотрите на спидометр иногда?
Вы же смотрите на спидометр иногда?
Интеграл это сумма бесконечно малых, которая выливается в полне конкретный объект.
Комментировать ответ…Комментировать…
Ruslan Y
309
Инженер электронной техники, программист. · 14 мая
Зенон, черепаха и Ахиллес давно, но, Ньютон совсем все разрушил, когда изобрел дифференциальное исчисление. Оно сильно изменило мировосприятие и научило мыслить.
Комментировать ответ…Комментировать…
Вячеслав Васюхин
Баню люблю и делаю · 14 июл
Интеграл — это Идея, а дифференциал — воплощение идеи на практике. Сам процесс воплощения и его результат имеет обратное влияние на саму изначальную Идею, так Идея меняется. Вот так вот всё в нашем Мире и волнуется, колеблется, воюет и успокаивается, что бы потом опять Идеей изменений прийти к стабильному равновесию. Всё равно!
1 эксперт не согласен
Александр
возражает
14 июля
Ответ не имеет никакого отношения к заданному вопросу.
Комментировать ответ…Комментировать…
Михаил
121
18 мар 2020
В отличие от других ответчиков я начну с интеграла, а не с производной. Интеграл в жизни имеет конкретный физический смысл. Это площадь фигуры ограниченной осью абцисс Х и графиком функции. Далеко от жизни? Сейчас приблизим. Представим себе машину, которая едет. Отложим по оси Х время в пути, а по Y — скорость в каждый, конкретный момент времени, и начертим график… Читать далее
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
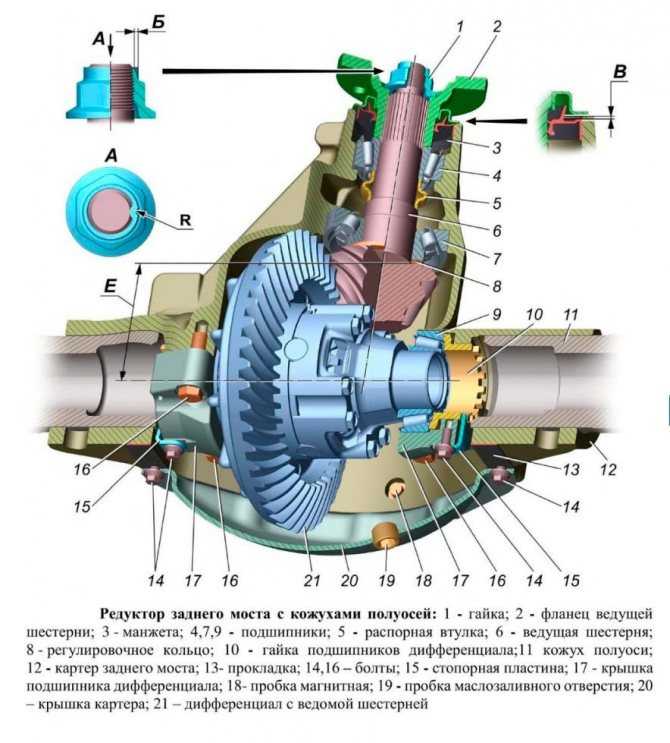
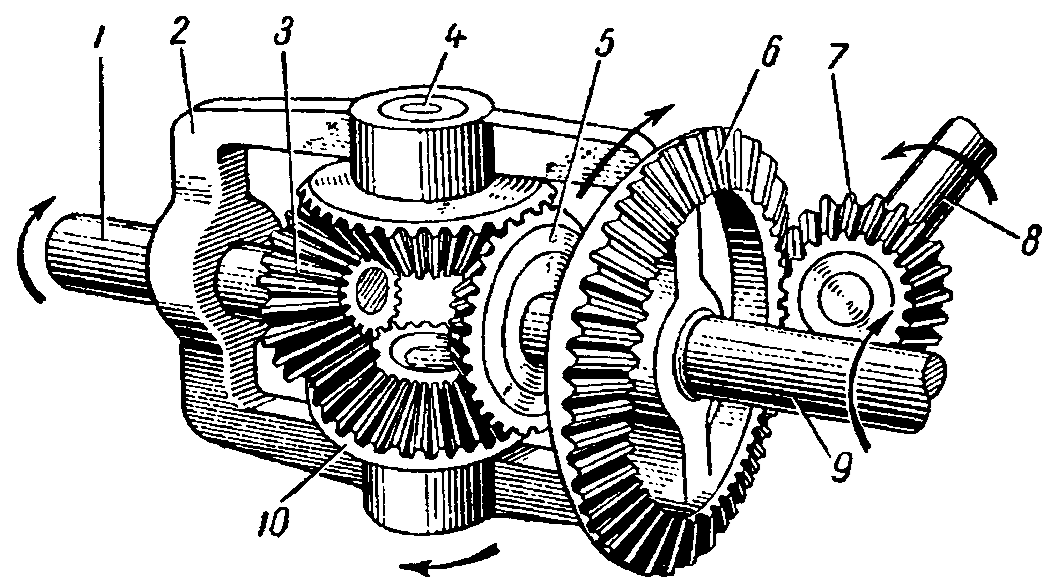
LSD дифференциал — что это, для чего нужен и как работает — TopWay.su
LSD дифференциал — что это, как работает и какую помощь может оказать на бездорожье? Дифференциал повышенного трения LSD работает также, как и аналогичные автоматические неполные блокировки. Он срабатывает в тех случаях, когда колеса на одной оси начинают крутиться со слишком разной по отношению друг к другу скоростью. Чаще всего LSD дифференциал ставят на внедорожники и спортивные автомобили, но считать его 100% блокировкой от застревания в грязи или диагонального вывешивания ошибочно.
Он срабатывает в тех случаях, когда колеса на одной оси начинают крутиться со слишком разной по отношению друг к другу скоростью. Чаще всего LSD дифференциал ставят на внедорожники и спортивные автомобили, но считать его 100% блокировкой от застревания в грязи или диагонального вывешивания ошибочно.
LSD дифференциал — что это такое
Как уже было сказано выше, дифференциал повышенного трения LSD не обеспечивает полной блокировки, допуская определенную разницу между скоростями вращения валов. Он срабатывает лишь в том случае, когда разница ощутима. Выше уже было сказано, что LSD часто ставят в различные автомобили: как в спортивные, так и во внедорожники
В пример можно привести LSD дифференциал Toyota — в определенный момент блокировка срабатывает и крутящий момент обеих валов сравнивается, становится одинаковым. Равные пропорции всё равно дают возможность завязшему колесу прокручиваться, но то колесо, которое имеет хорошее сцепление, тоже начинает крутиться и джип выезжает с засады на нормальное место (во многих, но далеко не во всех случаях).
Как работает LSD дифференциал и какие типы бывают
Классический — дифференциал чувствителен к разнице скоростей между валами, блокируя при определенном моменте. Это классическая блокировка, аналогичная вискомуфте. Применяется всё чаще, особенно во внедорожниках, так как лёгок в обслуживании и крайне прост по своей конструкции и принципу действия;
Традиционный — дифференциал срабатывает при разнице между передачей крутящего момента. Его уже почти никуда не устанавливают, встречается только на старых авто и то, чаще в нерабочем или полумертвом состоянии. Дифференциал LSD такого типа можно отнести к червячному типу, он блокирует автоматом при определенной разнице между КМ самого дифференциала и, непосредственно приводного вала.
Классический задний дифференциал LSD очень популярен, но на многих старых машинах доведен до ужасного состояния. В новые его тоже периодически устанавливают, но, как уже говорилось выше, его эффективность в серьезной грязи не очень высока. Многое зависит от прокладки между сиденьем и рулем, поэтому в умелых руках автомобиль лишь с такой блокировкой тоже способен на небольшие подвиги, но заменить 100% блокировку он не способен.
Многое зависит от прокладки между сиденьем и рулем, поэтому в умелых руках автомобиль лишь с такой блокировкой тоже способен на небольшие подвиги, но заменить 100% блокировку он не способен.
Также начинающие джиперы часто интересуются, как определить LSD дифференциал — делается это очень просто: задняя сторона машины домкратиться так, чтобы колеса отрывались от земли. Передняя часть авто при этом стоит на земле (не забывайте ставить под колеса противооткаты и держать авто на передаче в момент подъема). Колесо, которое оказывается в воздухе, можно попробовать покрутить. Если второе колесо крутится в ту же сторону, то у вас установлен LSD. Если второе колесо начинает крутиться в другую сторону, то в мосту или ничего нет, или дифференциал с блокировкой сломан и не функционирует. Также определить наличие или отсутствие LSD в мосту можно по наклейкам на самом узле или на арке водительской двери, но как показывает практика, чаще всего на старых авто такие наклейки не сохраняются.
TopWay.
 su — магазин внедорожного оборудования
su — магазин внедорожного оборудования
©
2022
определение слова «дифференциал» в The Free Dictionary.
«дифференциал».
прил.
1. Относящийся к или показывающий различие.
2. Создание или изменение; отличительный.
3. Зависит от конкретного различия или отличия или использует его.
4. Математика Дифференциация или относящаяся к ней.
5. Связанные с разницей в скорости или направлении движения.
н.
1. Математика
а. Бесконечно малое приращение переменной.
б. Произведение производной функции одной переменной на приращение независимой переменной.
2. Дифференциал.
3. Разница между сопоставимыми вещами, например, в размере заработной платы или в цене.
по-разному доп.
Словарь английского языка American Heritage®, пятое издание. Авторские права © 2016, издательство Houghton Mifflin Harcourt Publishing Company. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
дифференциальный
(ˌdɪfəˈrɛnʃəl)
прил.
1. из, относящийся к или использующий различие
2. представляющие собой разницу; различающие
3. (математика) математика , содержащие или включающие одну или несколько производных или дифференциалов
4. (общая физика) физика инженерное дело или основанные на них разница между двумя эффектами, движениями, силами и т. д.: дифференциальный усилитель.
д.: дифференциальный усилитель.
n
5. фактор, который отличает две сопоставимые вещи
6. (Математика) математика
а. приращение данной функции, выраженное как произведение производной этой функции и соответствующего приращения независимой переменной
b. приращение данной функции двух или более переменных, f( x 1, x 2, … x n ), выраженное как сумма произведений каждой частной производной и приращения соответствующей переменной
7. (Машиностроение) планетарная зубчатая передача, позволяющая двум валам вращаться с разными скоростями, при этом приводимый в движение третьим валом. См. также дифференциал
8. (Термины производственных отношений и управления персоналом) в основном Брит разница между ставками оплаты за разные виды труда, особенно при формировании структуры оплаты труда в отрасли
9. (Коммерция) (в торговле) разница в ставках, особенно между сопоставимыми трудовыми услугами или транспортными маршрутами
(Коммерция) (в торговле) разница в ставках, особенно между сопоставимыми трудовыми услугами или транспортными маршрутами
ˌdifferˈ включительно Adv
Коллинз английский словарь — полная и неисправная, 12 -е издание 2014 © Harpercollins Publishers 1991, 1994, 1998, 2000, 2003, 2006, 2007, 2011, 2014,
, Dif • FER • EN, EN, EN •tial
(ˌdɪf əˈrɛn ʃəl)
прил.
1. различия или разнообразия.
2. представляющие собой разницу; отличительный; отличительный.
3. демонстрирующий или зависящий от различия или различия.
4. относящиеся к разности двух или более движений, сил и т. д. или включающие их.
5. относящиеся к математическим производным или производным или включающие их.
н.
6. разница или величина разницы, как в скорости, стоимости, степени или качестве, между сопоставимыми вещами.
7. дифференциал.
8. Мат.
Мат.
а. функция двух переменных, которая получается из заданной функции, y = f ( x ), и которая выражает приблизительное приращение данной функции как произведение производной функции на приращение независимой переменной, записанное как dy = f~ ( x ) dx.
б. любое обобщение этой функции на более высокие измерения.
9. Физика. количественная разница между двумя или более силами, движениями и т. д.: перепад давления.
[1640–50; <средневековая латынь]
по-разному, нареч.
Рэндом Хаус Словарь колледжа Кернермана Вебстера, © 2010 K Dictionaries Ltd. Авторские права Random House, Inc., 2005, 1997, 1991. Все права защищены.
Переводы
дифференциалы
дифференциалы
Испанский словарь Коллинза — полное и полное, 8-е издание, 2005 г. © William Collins Sons & Co. Ltd., 1971, 1988 © HarperCollins Publishers, 1992, 1993, 1996, 1997, 2000, 2003, 2005
Collins English/French Electronic Resource. © HarperCollins Publishers 2005
© HarperCollins Publishers 2005
дифференциальный
прил. (= другой) ставки заработной платы, лечение, диагностика, последствия → unterschiedlich; (= отличительная черта) признак → непонятный; дифференциал Цена (Comm) → Preisdiskriminierung F
Дифференциал
:
Дифференциальный коэффициент
N (Math) → Abletung F
N (MATH) → Abletung F
Collins Nemcory Dabary —М. William Collins Sons & Co. Ltd. 1980 © HarperCollins Publishers 1991, 1997, 1999, 2004, 2005, 2007
Итальянский словарь Collins, 1-е издание © HarperCollins Publishers 1995
дифференциал
Англо-испанский медицинский словарь © Farlex 2012
AC Введение в дифференциальные уравнения
Мотивирующие вопросы
Что такое дифференциальное уравнение и какую информацию оно нам может дать?
Как возникают дифференциальные уравнения в окружающем нас мире?
Что мы подразумеваем под решением дифференциального уравнения?
В предыдущих главах мы видели, что производная функции говорит нам о скорости изменения функции. Основная теорема исчисления помогла нам определить общее изменение функции на интервале по скорости изменения функции. Например, скорость объекта говорит нам о скорости изменения положения этого объекта. Интегрируя скорость по интервалу времени, мы можем определить, насколько изменится положение за этот интервал времени. Если мы знаем, где находится объект в начале этого интервала, у нас достаточно информации, чтобы предсказать, где он будет в конце интервала.
Основная теорема исчисления помогла нам определить общее изменение функции на интервале по скорости изменения функции. Например, скорость объекта говорит нам о скорости изменения положения этого объекта. Интегрируя скорость по интервалу времени, мы можем определить, насколько изменится положение за этот интервал времени. Если мы знаем, где находится объект в начале этого интервала, у нас достаточно информации, чтобы предсказать, где он будет в конце интервала.
В этой главе мы вводим понятие дифференциальных уравнений . Дифференциальное уравнение — это уравнение, которое дает описание производной функции, что означает, что оно сообщает нам скорость изменения функции. Используя эту информацию, мы хотели бы узнать как можно больше о самой функции. В идеале мы хотели бы иметь алгебраическое описание функции. Как мы увидим, в некоторых ситуациях это может быть слишком много, но мы все же сможем сделать точные приближения.
Предварительный просмотр 7.1.1.
Положение движущегося объекта задается функцией \(s(t)\text{,}\), где \(s\) измеряется в футах, а \(t\) в секундах.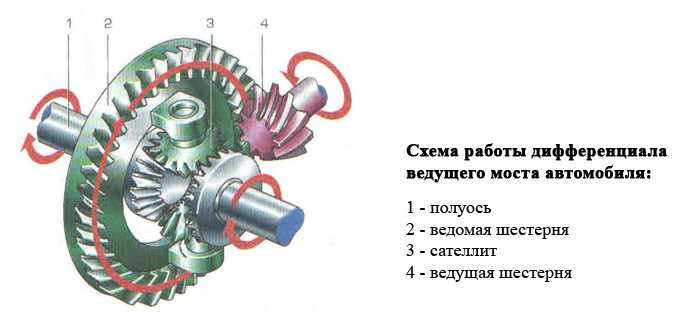 Определяем, что скорость равна \(v(t) = 4t + 1\) футов в секунду.
Определяем, что скорость равна \(v(t) = 4t + 1\) футов в секунду.
Насколько изменится позиция за интервал времени \([0,4]\text{?}\)
Дает ли это вам достаточно информации для определения \(s(4)\text{,}\) положения в момент времени \(t=4\text{?}\) Если да, то что такое \(s(4)) \text{?}\) Если нет, какую дополнительную информацию вам нужно знать, чтобы определить \(s(4)\text{?}\) 92 + t — 4\text{?}\) Объясните откуда вы это знаете.
Существуют ли другие возможности для \(s(t)\text{?}\) Если да, то какие?
Если в дополнение к знанию функции скорости \(v(t) = 4t+1\text{,}\) мы знаем начальное положение \(s(0)\text{,}\), сколько возможностей есть ли для \(s(t)\text{?}\)
Подраздел 7.1.1 Что такое дифференциальное уравнение?
Дифференциальное уравнение — это уравнение, описывающее производную или производные неизвестной нам функции. Например, уравнение
\begin{уравнение*}
\frac{dy}{dx} = x\sin x
\end{уравнение*}
описывает производную неизвестной нам функции \(y(x)\).
Поскольку многие важные примеры дифференциальных уравнений включают величины, которые изменяются во времени, независимой переменной в нашем обсуждении часто будет время \(t\text{.}\) В предварительном задании мы рассмотрели дифференциальное уравнение
\begin{уравнение*}
\frac{ds}{dt} = 4t + 1\text{.}
\end{уравнение*}
Зная скорость и начальное положение движущегося объекта, мы могли найти его положение в любой момент времени.
Поскольку дифференциальные уравнения описывают производную функции, они дают нам информацию о том, как эта функция изменяется. Нашей целью будет использование этой информации для прогнозирования значения функции в будущем; таким образом, дифференциальные уравнения дают нам что-то вроде хрустального шара.
Дифференциальные уравнения часто возникают в нашем повседневном мире. Например, вы можете услышать рекламу банка:
.
С нами ваши деньги будут расти на 3% годовых.
Это безобидное утверждение на самом деле является дифференциальным уравнением.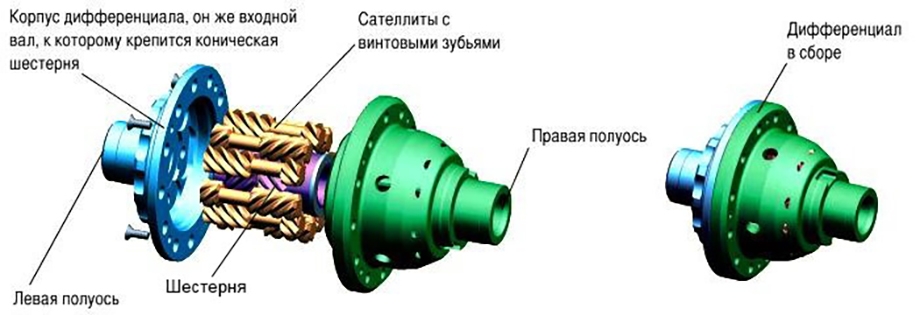 Давайте переведем: \(A(t)\) будет суммой денег, которую вы имеете на своем счету в момент времени \(t\text{.}\) Скорость, с которой ваши деньги растут, является производной \(dA/dt\text {,}\) и нам говорят, что эта скорость равна \(0,03 A\text{.}\) Это приводит к дифференциальному уравнению
Давайте переведем: \(A(t)\) будет суммой денег, которую вы имеете на своем счету в момент времени \(t\text{.}\) Скорость, с которой ваши деньги растут, является производной \(dA/dt\text {,}\) и нам говорят, что эта скорость равна \(0,03 A\text{.}\) Это приводит к дифференциальному уравнению
\begin{уравнение*}
\frac{dA}{dt} = 0,03 А\text{.}
\end{уравнение*}
Это дифференциальное уравнение имеет несколько иной смысл, чем предыдущее уравнение \(\frac{ds}{dt} = 4t+1\text{.}\) В предыдущем примере скорость изменения зависит только от независимой переменной \ (t\text{,}\) и мы можем найти \(s(t)\) путем интегрирования скорости \(4t+1\text{.}\) Однако в банковском примере скорость изменения зависит от зависимая переменная \(A\text{,}\), поэтому нам понадобятся некоторые новые методы, чтобы найти \(A(t)\text{.}\)
Мероприятие 7.1.2.
Выразите следующие утверждения в виде дифференциальных уравнений. В каждом случае вам нужно будет ввести обозначения для описания важных величин в утверждении, поэтому обязательно четко укажите, что означает ваше обозначение.
Население города постоянно увеличивается на 1,25% в год.
Каждый день радиоактивный образец теряет в массе 5,6% своей массы.
У вас есть банковский счет, на который каждый год постоянно начисляется 4% годовых. При этом вы постоянно снимаете деньги со счета по ставке $1000 в год. 9\круг\) комната. Температура соды непрерывно нагревается со скоростью 10% разницы между температурой соды и температурой в комнате каждую минуту.
Подраздел 7.1.2 Дифференциальные уравнения в окружающем нас мире
Дифференциальные уравнения дают естественный способ описания явлений, которые мы наблюдаем в реальном мире. Например, физические принципы часто выражаются как описание того, как изменяется величина. Хорошим примером является второй закон Ньютона, который гласит:
Произведение массы объекта на ускорение равно приложенной к нему силе.
Например, когда гравитация действует на объект вблизи земной поверхности, она оказывает силу, равную \(mg\text{,}\) массе объекта, умноженной на гравитационную постоянную \(g\text{. }\) Таким образом, у нас есть
}\) Таким образом, у нас есть
\начать{выровнять*}
ma =\mathstrut\amp мг, \\text{или}\\
\frac{dv}{dt} =\mathstrut \amp g\text{,}
\конец{выравнивание*}
, где \(v\) — скорость объекта, а \(g = 9.8\) метров в секунду в квадрате. Обратите внимание, что этот физический принцип говорит нам не о том, какова скорость объекта, а о том, как скорость объекта изменяется.
Мероприятие 7.1.3.
Ниже показаны два графика, отображающие скорость падающих объектов. Слева скорость парашютиста, а справа скорость метеорита, входящего в атмосферу Земли.
Рисунок 7.1.1. Скорость парашютиста. Рис. 7.1.2. Скорость метеорита.
Начните со скорости парашютиста и используйте данный график для измерения скорости изменения \(dv/dt\), когда скорость равна \(v=0,5, 1,0, 1,5, 2,0\text{,}\) и \(2,5 \text{.}\) Нанесите свои значения на график ниже. Вы должны хорошенько подумать об этом: вы строите производную \(dv/dt\) как функцию скорости .
Теперь проделайте то же самое со скоростью метеорита: используйте данный график для измерения скорости изменения \(dv/dt\), когда скорость равна \(v=3.
 5,4.0,4.5\text{,}\) и \(5.0\text{.}\) Нанесите свои значения на график выше.
5,4.0,4.5\text{,}\) и \(5.0\text{.}\) Нанесите свои значения на график выше.Вы должны обнаружить, что все ваши точки лежат на прямой. Напишите уравнение этой прямой, используя правильные обозначения для величин на горизонтальной и вертикальной осях.
Зависимость, которую вы только что нашли, представляет собой дифференциальное уравнение. Напишите полное предложение, объясняющее его значение.
Глядя на дифференциальное уравнение, определите значения скорости, при которых скорость увеличивается.
По дифференциальному уравнению определите значения скорости, при которых скорость уменьшается.
Используя дифференциальное уравнение, определите значения скорости, при которых скорость остается постоянной.
Целью этого занятия является демонстрация того, как дифференциальные уравнения моделируют процессы в реальном мире. В этом примере на скорость влияют два фактора: сила тяжести и сопротивление ветра. {-0,5t}\) решением 9{-0.5t}\text{.}\) На рисунке 7.1.3 мы видим графики этих решений для нескольких значений \(C\text{,}\) с пометками.
{-0,5t}\) решением 9{-0.5t}\text{.}\) На рисунке 7.1.3 мы видим графики этих решений для нескольких значений \(C\text{,}\) с пометками.
Рисунок 7.1.3. Семейство решений дифференциального уравнения \(\frac{dv}{dt} = 1,5 — 0,5v\text{.}\)
Обратите внимание, что значение \(C\) связано с начальным значением скорости \(v(0)\text{,}\), поскольку \(v(0) = 3+C\text{.}\) Другими словами, в то время как дифференциальное уравнение описывает, как скорость изменяется в зависимости от скорости самой по себе этой информации недостаточно для однозначного определения скорости: нам нужно знать еще и начальную скорость. По этой причине дифференциальные уравнения обычно имеют бесконечно много решений, по одному для каждого начального значения. Мы видели это явление раньше: зная скорость движущегося объекта \(v(t)\text{,}\), мы не можем однозначно определить функцию положения объекта, если мы также не знаем его начальное положение.
Если нам дано дифференциальное уравнение и начальное значение неизвестной функции, мы говорим, что имеем задачу с начальным значением. Например,
Например,
\begin{уравнение*}
\frac{dv}{dt} = 1,5-0,5v, \v(0) = 0,5
\end{уравнение*}
— проблема с начальным значением. В этой задаче мы знаем значение \(v\) в определенный момент времени и знаем, как меняется \(v\). Следовательно, должна существовать ровно одна функция \(v\), удовлетворяющая задаче о начальных значениях.
Это демонстрирует следующее важное общее свойство задач с начальными значениями.
Задачи с начальным значением, которые «хорошо себя ведут», имеют ровно одно решение, которое существует в некотором интервале вокруг начальной точки.
Мы не будем беспокоиться о том, что означает «хорошее поведение» — это техническое условие, которому будут удовлетворять все дифференциальные уравнения, которые мы рассматриваем.
В заключение этого раздела отметим, что дифференциальные уравнения можно классифицировать на основе определенных характеристик, которыми они могут обладать. Вы можете увидеть много различных типов дифференциальных уравнений в более позднем курсе дифференциальных уравнений. Сейчас мы хотели бы ввести несколько терминов, которые используются для описания дифференциальных уравнений. 92} = -10 лет
Сейчас мы хотели бы ввести несколько терминов, которые используются для описания дифференциальных уравнений. 92} = -10 лет
\end{уравнение*}
— уравнение второго порядка.
Дифференциальное уравнение является автономным , если независимая переменная не фигурирует в описании производной. Например,
\begin{уравнение*}
\frac{dv}{dt} = 1,5-0,5v
\end{уравнение*}
является автономным, поскольку описание производной \(dv/dt\) не зависит от времени. Уравнение
\begin{уравнение*}
\frac{dy}{dt} = 1,5t — 0,5y\text{,}
\end{уравнение*}
Однако
не является автономным.
Подраздел 7.1.4 Резюме
Дифференциальное уравнение — это просто уравнение, описывающее производную(ые) неизвестной функции.
Физические принципы, а также некоторые повседневные ситуации часто описывают, как изменяется величина, что приводит к дифференциальным уравнениям.
Решением дифференциального уравнения является функция, производная которой удовлетворяет описанию уравнения.
 Дифференциальные уравнения обычно имеют бесконечно много решений, параметризованных начальными значениями. 9{-Акт}\)
Дифференциальные уравнения обычно имеют бесконечно много решений, параметризованных начальными значениями. 9{-Акт}\)
4.
Предположим, что \(T(t)\) представляет собой температуру чашки кофе, поставленной в комнате, где \(T\) выражается в градусах по Фаренгейту, а \(t\) в минутах. Физический принцип, известный как закон охлаждения Ньютона, говорит нам, что
\begin{уравнение*}
\frac{dT}{dt}= -\frac1{15}T+5\text{.}
\end{уравнение*}
Предположим, что \(T(0)=105\text{.}\) Что дает нам дифференциальное уравнение для значения \(\frac{dT}{dt}\vert_{T=105}\text {?}\) Объясните полным предложением значение этих двух фактов.
Увеличивается или уменьшается \(T\) при \(t=0\text{?}\)
Какова примерная температура в \(t=1\text{?}\)
На графике ниже постройте график зависимости \(dT/dt\) от \(T\text{.}\)
При каких значениях \(T\) \(T\) увеличивается? При каких значениях \(Т\) \(Т\) убывает?
Как вы думаете, какая температура в комнате? Объясните свое мышление.

9{-t/15}\) — решение дифференциального уравнения с начальным значением \(T(0) = 105\text{.}\) Что происходит с этим решением спустя долгое время?
5.
Предположим, что популяция определенного вида описывается функцией \(P(t)\text{,}\), где \(P\) выражается в миллионах. Предположим далее, что скорость изменения населения определяется дифференциальным уравнением
\begin{уравнение*}
\frac{dP}{dt} = f(P)
\end{уравнение*}
, где \(f(P)\) — функция, показанная ниже.
При каких значениях населения \(P\) население увеличивается?
При каких значениях населения \(P\) население уменьшается?
Если \(P(0) = 3\text{,}\), как будет меняться население во времени?
Если начальная популяция удовлетворяет \(0\lt P(0)\lt 1\text{,}\), что произойдет с популяцией через очень долгое время?
Если начальная популяция удовлетворяет \(1\lt P(0)\lt 3\text{,}\), что произойдет с популяцией через очень долгое время?
Если начальная популяция удовлетворяет \(3\lt P(0)\text{,}\), что произойдет с популяцией через очень долгое время?
Эту модель роста населения иногда называют «ростом с порогом».

 su — магазин внедорожного оборудования
su — магазин внедорожного оборудования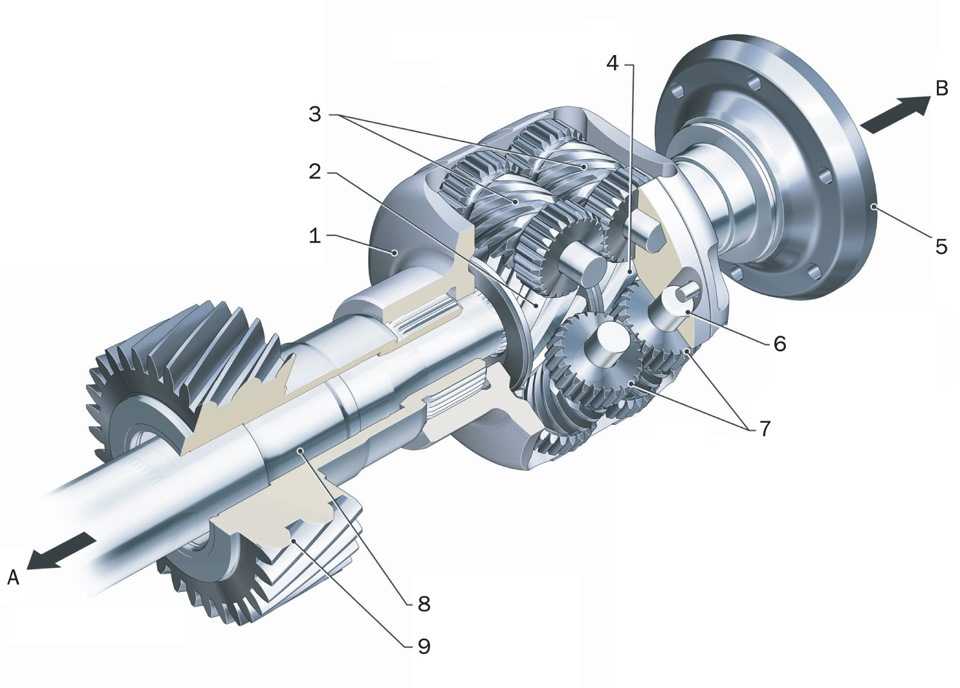 5,4.0,4.5\text{,}\) и \(5.0\text{.}\) Нанесите свои значения на график выше.
5,4.0,4.5\text{,}\) и \(5.0\text{.}\) Нанесите свои значения на график выше. Дифференциальные уравнения обычно имеют бесконечно много решений, параметризованных начальными значениями. 9{-Акт}\)
Дифференциальные уравнения обычно имеют бесконечно много решений, параметризованных начальными значениями. 9{-Акт}\)