Что такое крутящий момент: Что такое крутящий момент

Что такое крутящий момент

Крутящий момент двигателя является произведением силы на плечо рычага, к которому она прикладывается. Стоит напомнить, что сила измеряется в Ньютонах (Н), а плечо рычага в метрах (м). Расскажем о нем более подробно далее.

Очень многие автомобилисты не знают, что такое крутящий момент двигателя. На самом деле ответ на этот вопрос содержится еще в школьном курсе физики, но в свете того, что не все ее учили, а те, кто учил, не все поняли, а остальные просто забыли понятое, нет ничего удивительного, что этот вопрос остается открытым. Итак, что же такое крутящий момент двигателя?

Крутящий момент

Начать следует все же с физики. Крутящий момент двигателя является произведением силы на плечо рычага, к которому она прикладывается. Стоит напомнить, что сила измеряется в Ньютонах (Н), а плечо рычага в метрах (м). То есть один Нм равняется одному Ньютону (1Н), который приложен к метровому рычагу (1м).

В двигателе внутреннего сгорания сила передается от воспламеняющегося топлива поршню, от него к кривошипному механизму, а от него к коленвалу. Последний через систему трансмиссии и приводов и приводит колеса во вращение.

Разумеется, он не является постоянным и увеличивается, когда на плечо действует большая сила, и слабеет при ее уменьшении. Иными словами, когда водитель давит на «газ», то действующая на плечо сила возрастает и, соответственно, возрастает и крутящий момент.

Мощность двигателя

Крутящий момент имеет непосредственное отношение к мощности двигателя. Последняя, если говорить предельно просто, является совершенной за некоторую единицу времени работой. А поскольку работой двигателя и является тот самый крутящий момент, то мощность указывает на то, сколько раз за единицу времени двигателем был совершен крутящий момент.

Физиками была создана формула, связывающая оба этих показателя:

Мощность (P) = момент крутящий (Мкр) * измеряемые в об./мин обороты двигателя (N)/9549.

Хотя мощность измеряется в киловаттах, в нашей стране они довольно сложны для автомобилистов, поэтому ее, как правило, измеряют в лошадиных силах (л. с.). Ничего сложного здесь нет, просто чтобы киловатты стали «лошадями», количество киловатт умножается на 1,36.

Крутящий момент и мощность

С каждым из этих компонентов вроде бы понятно, но на что влияет каждый из них? Мощность оказывает влияние на преодоление всевозможных сил, которые оказывают автомобилю противодействие. Таковыми являются силы качения колес, аэродинамические силы, и, конечно же, сила трения в трансмиссии, приводах машины, в самом двигателе и не только. И чем выше мощность двигателя, тем большее сопротивление машина в состоянии преодолеть и, соответственно, тем большую скорость разовьет. Однако мощность не является постоянной силой и сильно зависит от оборотов двигателя. Мощность на холостом ходу и на максимальных оборотах неодинакова. Поэтому многие автопроизводители указывают в технических характеристиках при каких оборотах достигается максимум мощности.

Здесь следует помнить, что максимальная мощность развивается не одномоментно, и с места машина стартует при минимальных оборотах, которые едва превышают холостой ход. Для того же чтобы мобилизировать максимум мощности необходим некоторый отрезок времени и именно здесь на сцену выходит крутящий момент. Именно он «решает» за какой временной промежуток автомобилем будет достигнута максимальная мощность. Проще говоря, динамика разгона автомобиля зависит именно от крутящего момента.

Бензиновые и дизельные двигатели

У бензиновых двигателей показатели не самые высокие. Своих почти максимальных значений бензиновый двигатель может достичь при оборотах, в среднем, 3-4 тысячи. Однако бензиновый двигатель способен быстро увеличивать мощность, и раскручиваться до семи и даже восьми тысяч оборотов. И если принять во внимание вышеприведенные формулы, то становится ясно, что при таких оборотах мощность может возрасти в несколько раз.

Что касается дизельных двигателей, то высокими оборотами они не обладают и как правило, их максимум составляет пять, а то и всего три тысячи оборотов. В этом отношении «дизель» однозначно проигрывает бензиновому двигателю. Но зато крутящий момент у дизельного двигателя в несколько раз превышает аналогичный показатель бензинового собрата и вдобавок он доступен почти с холостого хода.

Что важнее: крутящий момент или мощность?

Чтобы разобраться с этой задачей, можно привести несложный пример. Скажем, можно взять два двигателя от фирмы AUDI, один бензиновый 2.0 FSI (крутящий момент – 200 Нм, мощность – 150 л.с.), а другой дизельный (мощностью 140 л.с. и с крутящим моментом 320 Нм). После проведения тестирования в различных режимах оказывается, что дизельный двигатель мощнее бензинового двигателя в диапазоне от 1 до 4,5 тысяч оборотов. Причем мощность будет выше на 30, а то и на 40 «лошадей», что не мало.

Из этого следует, что обращать внимание исключительно на мощность не стоит, поскольку нередко менее объемный двигатель, имеющий более высокий крутящий момент, оказывается гораздо динамичнее, чем двигатель с низким крутящим моментом (пусть даже большого объема).

Подводя итоги можно сказать, что в корне неверно классифицировать автомобили ориентируясь исключительно на мощность (л.с.) двигателя. Кроме мощности необходимо учитывать еще и крутящий момент (Нм) поскольку если последний показатель будет намного выше, чем у другого автомобиля, то и двигатель у него будет значительно динамичнее.

Крутящий момент, что это и зачем он нужен?

Каждый двигатель внутреннего сгорания рассчитан на определенную максимальную мощность, которую он может выдавать при наборе определенного количества оборотов коленчатого вала. Однако помимо максимальной мощности существует еще и такая величина в характеристике двигателя, как максимальный крутящий момент, достигаемый на оборотах отличных от оборотов максимальной мощности.

Что же означает понятие крутящий момент? Говоря научным языком, крутящий момент равен произведению силы на плечо ее применения и измеряется в ньютон — метрах. Значит если к гаечному ключу длиной 1 метр (плечо), приложить силу в 1 Ньютон (перпендикулярно на конце ключа), то мы получим крутящий момент равный 1 Нм.

Для наглядности: если гайка затянута с усилием 3 кгс, то для ее откручивания придется к ключу с длиной плеча в 1 метр приложить усилие 3 кг. Однако, если на ключ длиной 1 метр надеть дополнительно 2-х метровый отрезок трубы, увеличив тем самым рычаг до 3 метров, то тогда для отворачивания этой гайки потребуется лишь усилие в 1 кг. Так поступают многие автолюбители при откручивании колесных болтов: либо добавляют отрезок трубы, а за неимением такового просто надавливают на ключ ногой, увеличив тем самым силу приложения к баллонному ключу. Так же если на рычаг метровой длины повесить груз равный 10 кг, то появится крутящий момент равный 10 кгм. В системе СИ это значение (перемножается на ускорение свободного падениям) будет соответствовать 98,1 Нм. Результат всегда един — крутящий момент, это произведение силы на длину рычага, стало быть, нужен либо длиннее рычаг, либо большее количество прикладываемой силы.

Все это хорошо, но для чего нужен крутящий момент в автомобиле и как его величина влияет на его поведение на дороге? Мощность двигателя лишь косвенно отражает тяговые возможности мотора, и ее максимальное значение проявляется, как правило, на максимальных оборотах двигателя.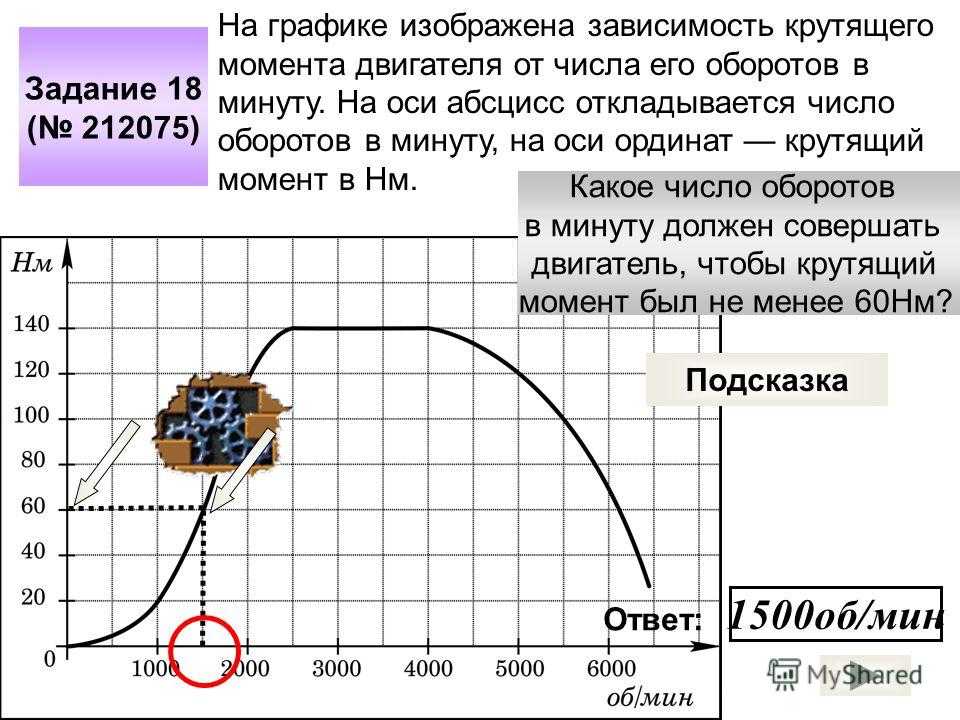 В реальной жизни в таких режимах практически никто не ездит, а вот ускорение двигателю требуется всегда и желательно с момента нажатия на педаль газа. На практике одни автомобили уже с низких оборотов ведут себя достаточно резво, другие напротив предпочитают лишь высокие обороты, а на низах показывают вялую динамику. Так у многих возникает масса вопросов, когда они с авто с бензиновым мотором мощностью 105-120 л.с. пересаживаются на 70-80 – сильный дизель, то последний с легкостью обходит машину с бензиновым мотором. Как такое может быть? Связано это с величиной тяги на ведущих колесах, которая различна для этих двух автомобилей. Величина тяги напрямую зависит от произведения таких показателей как, величины крутящего момента, передаточного числа трансмиссии, ее КПД и радиуса качения колеса. Как создается крутящий момент в двигателе. В двигателе нет метровых рычагов и грузов, и их заменяет кривошипно-шатунный механизм с поршнями.

Крутящий момент в двигателе образуется за счет сгорания топлива — воздушной смеси, которая расширяясь в объеме с усилием толкает поршень вниз. Поршень в свою очередь через шатун передает давление на шейку коленчатого вала. В характеристике двигателя нет значения плеча, но есть величина хода поршня (двойное значение радиуса кривошипа коленвала). Для любого мотора крутящий момент рассчитывается следующим образом. Когда поршень с усилием 200 кг двигает шатун на плечо 5 см, появляется крутящий момент 10 кГс или 98,1Нм. В данном случает для увеличения крутящего момента нужно либо увеличить радиус кривошипа, или же увеличить давление расширяющихся газов на поршень. До определенной величины можно увеличить радиус кривошипа, но будут расти и размеры блока цилиндров как в ширину, так и в высоту и увеличивать радиус до бесконечности невозможно. Да и конструкцию двигателя придется значительно упрочнять, так как будут нарастать силы инерции и другие отрицательные факторы. Следовательно, у разработчиков моторов остался второй вариант – нарастить силу, с которой поршень передает усилие для прокручивания коленвала. Для этих целей в камере сгорания нужно сжечь больше горючей смеси и к тому же более качественно. Для этого меняют величину и конфигурацию камеры сгорания, делают «вытеснители» на головках поршней и повышают степень сжатия. Однако максимальный крутящий момент доступен не на всех оборотах мотора и у различных двигателей пик момента достигается на различных режимах. Одни моторы выдают его в диапазоне 1800- 3000 об/мин, другие на 3000-4500 об/мин. Это зависит от конструкции впускного коллектора и фаз газораспределения, когда эффективное наполнение цилиндров рабочей смесью происходит при определенных оборотах.

Наиболее простое решение для увеличения крутящего момента, а следовательно и тяги, это применение турбо или механического наддува, либо применение их в комплексе. Тогда крутящий момент можно уже использовать с 800-1000 об/мин, т.е. практически сразу. К тому же это закрывает такую проблему, как провалы при наборе скорости, так как величина крутящего момента становится практически одинакова во всем диапазоне оборотов двигателя. Достигается это различными путями: увеличивают количество клапанов на цилиндр, делают управляемыми фазы газораспределения для оптимизации сгорания топлива, повышают степень сжатия, применяют выпускной коллектор по формуле 1-4 -2-3, в турбинах применяют крыльчатки с изменяемым и регулируемым углом атаки лопаток и т. д.

Учебное пособие по крутящему моменту и вращательному движению

Что такое крутящий момент?

Крутящий момент — это мера того, насколько сила, действующая на объект, заставляет этот объект вращаться. Объект вращается вокруг оси, которую мы назовем точкой поворота и обозначим ‘\(O\)’. Мы будем называть силу ‘\(F\)’. Расстояние от точки вращения до точки, где действует сила, называется плечом момента и обозначается «\(r\)». Обратите внимание, что это расстояние ‘\(r\)’ также является вектором и указывает от оси вращения до точки, где действует сила. (Обратитесь к рисунку 1 для графического представления этих определений.)

Рисунок 1: Определения

Крутящий момент определяется как  \(\Gamma = r \times F = rF \sin (\theta)\).

Другими словами, крутящий момент представляет собой перекрестное произведение между вектором расстояния (расстояние от точки вращения до точки приложения силы) и вектором силы, где ‘\(a\)’ представляет собой угол между \(r\) и \(F. \)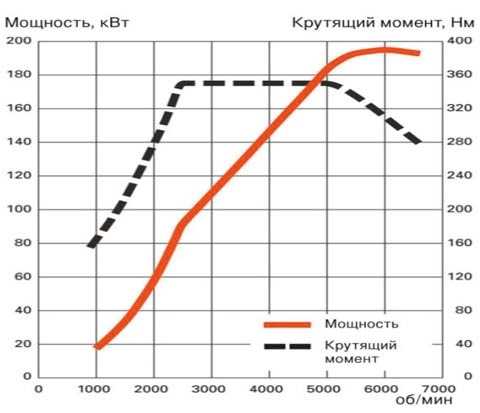

Перекрестное произведение

Перекрестное произведение, также называемое векторным произведением, представляет собой операцию над двумя векторами. Перемножение двух векторов дает третий вектор, который перпендикулярен плоскости, в которой лежат первые два. То есть для пересечения двух векторов \(A\) и \(B\) мы размещаем \(A\) и \(B\) так, чтобы их хвосты находились в одной точке. Затем их векторное произведение \(A \times B\) дает третий вектор, скажем, \(C\), хвост которого также находится в той же точке, что и у \(A\) и \(B.\) Вектор \(C\) указывает направление, перпендикулярное (или нормальное) к обоим \(A\) и \(B). Направление \(C\) зависит от правила правой руки.

Рисунок CP 1: \(A \times B = C\)

Если угол между \(A\) и \(B\) равен , то векторное произведение \(A\) и \(B\ ) можно выразить как 

\(A \times B = A B \sin(\theta)\)

Рисунок CP2: \(B \times A = D\)

Если компоненты для векторов \(A\) и \ (B\) известны, то мы можем выразить компоненты их векторного произведения, \(C = A \times B\) следующим образом A_xB_z\)
\(C_z = A_xB_y — A_yB_x\)
 
Далее, если вы знакомы с определителями, \(A \times B\), равно 

\(A \times B = \Biggr| \begin {matrix} i \quad j \quad k \\ A_x \; A_y \; A_z \\ B_x \; B_y \; B_z \end{matrix} \Biggr|\)

Сравнивая рисунки CP1 и CP2, мы замечаем, что 
\(A \times B = — B \times A\)

Очень хорошая симуляция, позволяющая исследовать свойства перекрестного произведения, доступна по ссылке ЗДЕСЬ. Используйте кнопку «назад», чтобы вернуться в это место.

Используя правило правой руки , мы можем найти направление вектора крутящего момента. Если мы направим пальцы в направлении \(r,\) и согнем их в направлении \(F,\), то большой палец будет указывать в направлении вектора крутящего момента.

Правило правой руки

Вопрос

В каком направлении крутящий момент на этой диаграмме относительно точки вращения, обозначенной \(O\)?

Рисунок RHR 1: Схема проблемы Рисунок RHR 2: Схема проблемы, сила была преобразована, чтобы упростить использование правила правой руки

Решение

Здесь мы предполагаем, что векторы силы \(F,\) и плеча момента r были первоначально размещены «голова к голове» (то есть, \(F\) указывал на острие стрелки \(r,\) не в своей точке вращения). Это показано на рис. RHR 1. Однако, переводя вектор силы в его положение на рис. RHR 2, использование правила правой руки становится более очевидным.

Без этого уточнения можно интерпретировать рисунок RHR 2 как вектор силы, проходящий через точку вращения, и в этом случае крутящего момента не будет. Это связано с определением плеча момента, которое представляет собой расстояние между точкой вращения и точкой, в которой действует сила. Если сила действует прямо на точку вращения, то \(r = 0,\), поэтому крутящего момента не будет. (Имея плечо момента, равное нулю, это все равно, что пытаться открыть дверь, нажимая на ее петли; ничего не происходит, потому что приложенная сила не создает крутящего момента.)

Вспомните использование правила правой руки при расчете крутящего момента. Пальцы должны быть направлены в сторону первого вектора и согнуты в сторону второго вектора. В этом случае крутящий момент представляет собой перекрестное произведение плеча момента и крутящего момента. Таким образом, пальцы будут указывать в том же направлении, что и плечо момента, и свернуты в направлении силы (по часовой стрелке). Направление вашего большого пальца — это направление крутящего момента; в этом случае крутящий момент попадает на экран.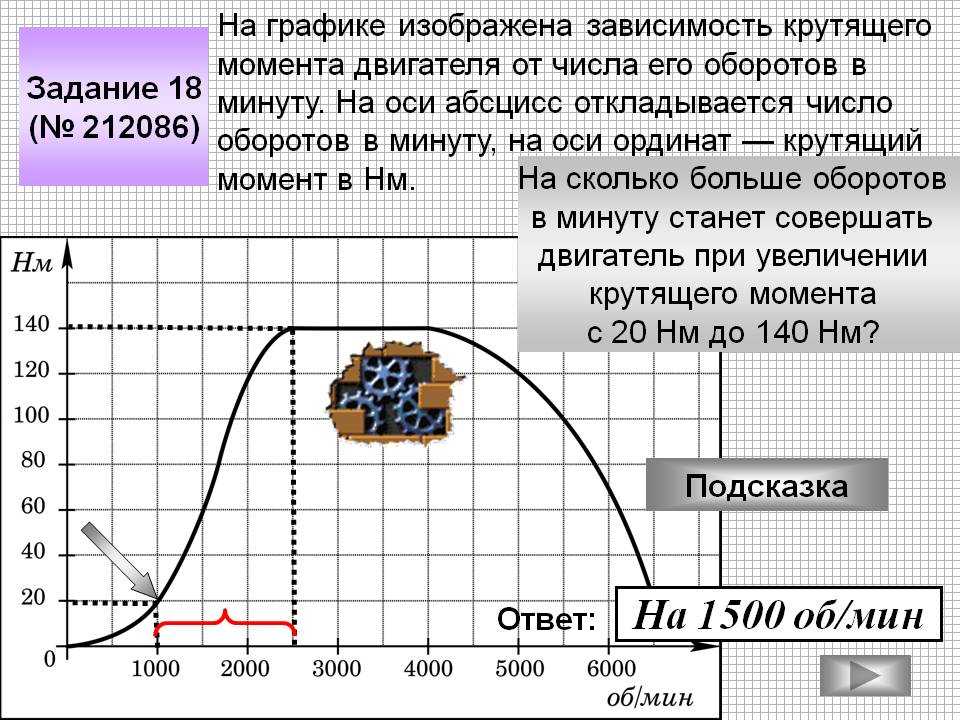

Мы можем представить «внутри» и «из» с помощью символов при рисовании трехмерных диаграмм. Символ «в» – это  (предполагается, что это конец стрелки), а «из» –  (это кончик стрелки).

Рисунок RHR 3: Схема решенной проблемы (результирующий крутящий момент находится на экране)

Представьте, что вы толкаете дверь, чтобы открыть ее. Сила вашего толчка (\(F\)) заставляет дверь вращаться вокруг своих петель (точка вращения, \(O\)). То, насколько сильно вам нужно нажимать, зависит от расстояния, на котором вы находитесь от петель (\(r\)) (и от нескольких других вещей, но давайте их сейчас проигнорируем). Чем ближе вы к петлям (т.е. чем меньше \(r\)), тем труднее нажимать. Вот что бывает, когда пытаешься толкнуть дверь не с той стороны. Крутящий момент, создаваемый вами на двери, меньше, чем если бы вы отодвинули правильную сторону (от ее петель).

Обратите внимание, что приложенная сила \(F,\) и плечо момента \(r,\) не зависят от объекта. Кроме того, сила, приложенная к точке поворота, не вызовет крутящего момента, поскольку плечо момента будет равно нулю (\(r = 0\)).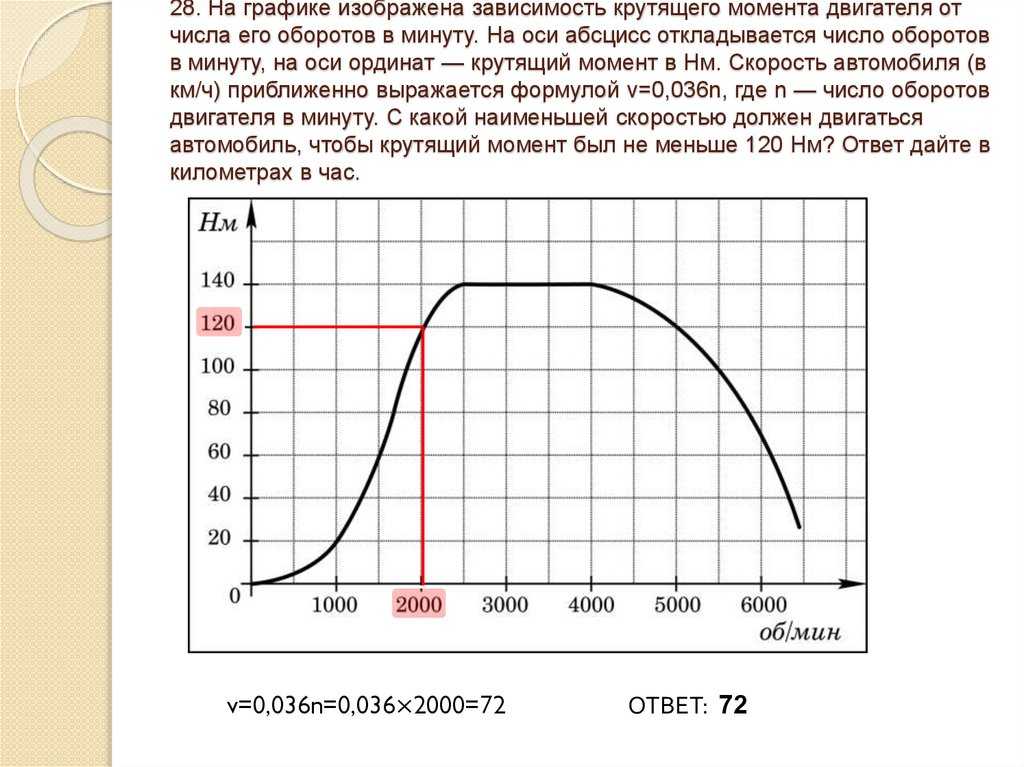

Другой способ выражения приведенного выше уравнения состоит в том, что крутящий момент является произведением величины силы и перпендикулярного расстояния от силы до оси вращения (т.е. точки поворота).

Пусть сила, действующая на объект, разбита на тангенциальную (\(F_{tan}\)) и радиальную (\(F_{rad}\)) составляющие (см. рис. 2). (Обратите внимание, что тангенциальная составляющая перпендикулярна плечу момента, а радиальная составляющая параллельна плечу момента.) Радиальная составляющая силы не влияет на крутящий момент, поскольку она проходит через точку поворота. Таким образом, только тангенциальная составляющая силы влияет на крутящий момент (поскольку она перпендикулярна линии между точкой действия силы и точкой поворота).

Рисунок 2: Тангенциальная и радиальная составляющие силы F

На объект может действовать более одной силы, и каждая из этих сил может действовать на разные точки объекта. Тогда каждая сила будет вызывать крутящий момент. Чистый крутящий момент представляет собой сумму отдельных крутящих моментов.

Вращательное равновесие аналогично поступательному равновесию, где сумма сил равна нулю. При вращательном равновесии сумма крутящих моментов равна нулю. Другими словами, на объекте нет чистого крутящего момента.

\(\sum \tau = 0\)

Обратите внимание, что единицами крутящего момента в системе СИ является ньютон-метр , что также является способом выражения джоуля (единицы измерения энергии). Однако крутящий момент — это не энергия. Итак, чтобы избежать путаницы, мы будем использовать единицы Н·м, а не Дж. Различие возникает из-за того, что энергия — это скалярная величина, а крутящий момент — это вектор.

Полезное и интересное интерактивное занятие по вращательному равновесию.

Крутящий момент и угловое ускорение

В этом разделе мы разработаем взаимосвязь между крутящим моментом и угловым ускорением. Для этого раздела вам необходимо иметь общее представление о моментах инерции.

Момент инерции

Момент инерции является аналогом массы при вращении. Просмотрите определения, как объяснено в вашем учебнике.

В следующей таблице приведены моменты инерции для различных обычных тел. «М» в каждом случае — это общая масса объекта. 92\)

Рис. 3. Радиальная и тангенциальная составляющие силы, два измерения

Представьте себе силу F, действующую на некоторый объект на расстоянии r от его оси вращения. Мы можем разбить силу на тангенциальную (\(F_{tan}\)), радиальную (\(F_{rad}\)) (см. рис. 3). (Это предполагает двумерный сценарий. Для трех измерений — более реалистичной, но и более сложной ситуации — у нас есть три компонента силы: тангенциальная составляющая \(F_{tan}\), радиальная составляющая \( F_{rad}\) и z-компонента \(F_z\). Все компоненты силы взаимно перпендикулярны или нормальны.) 92\), умноженное на угловое ускорение, \(\альфа\).

\(\sum \tau = I\cdot \alpha\)

Панель 4: Радиальная, тангенциальная и z-компоненты силы, три измерения

Если провести аналогию между поступательным и вращательным движением, то это соотношение между угловое ускорение аналогично второму закону Ньютона.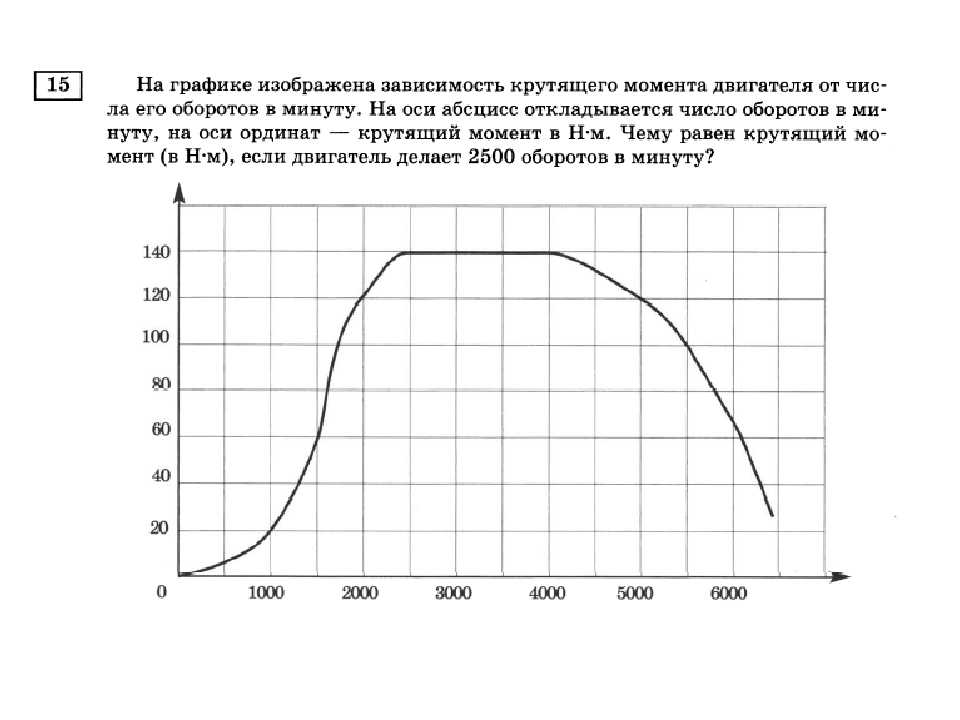 А именно, принимая крутящий момент за аналог силы, момент инерции за аналог массы и угловое ускорение за аналог ускорения, мы получаем уравнение, очень похожее на второй закон.

Пример задачи: Качающаяся дверь

Вопрос

В спешке, чтобы поймать такси, вы мчитесь через плавно вращающуюся дверь на тротуар. Сила, которую вы приложили к двери, была \(50 Н,\) приложена перпендикулярно плоскости двери. Ширина двери \(1,0\;м\). Предполагая, что вы толкнули дверь за ее край, каков был крутящий момент на распашной двери (принимая петлю за точку опоры)?

Подсказки

1. Где точка поворота?
2. Какая сила была приложена?
3. На каком расстоянии от точки вращения была приложена сила?
4. Какой угол между дверью и направлением силы?

Решение

Точка поворота находится на петлях двери, напротив того места, где вы толкали дверь. Сила, которую вы использовали, была \(50 Н,\) на расстоянии \(1,0\;м\) от точки вращения.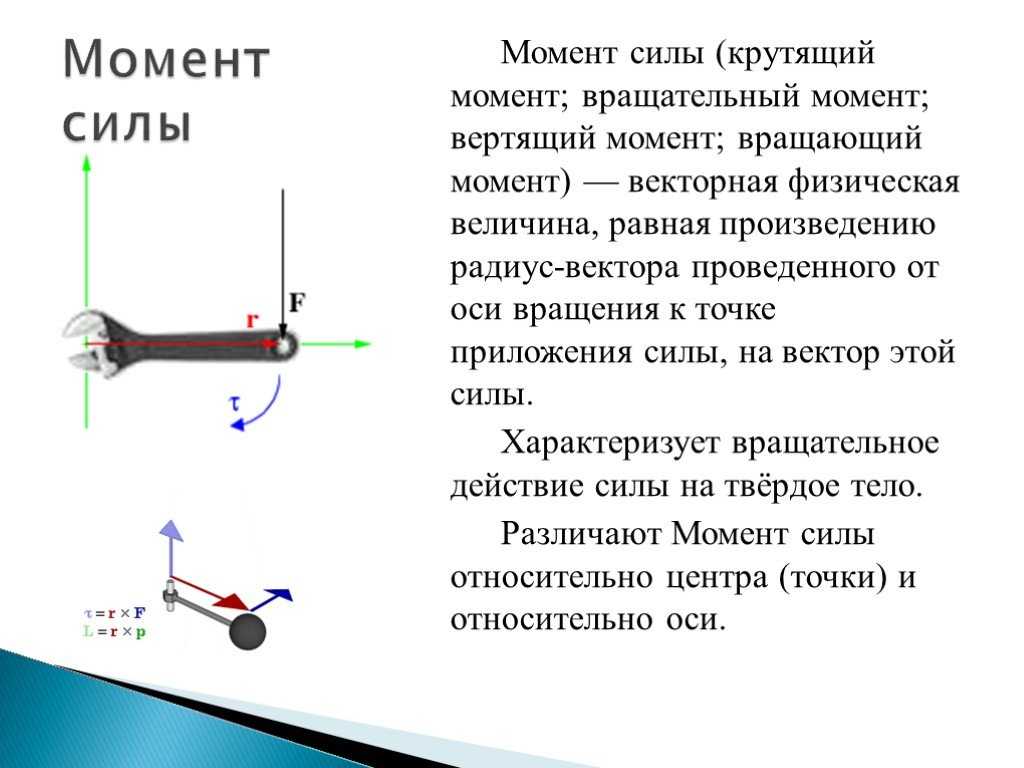 Вы ударили по двери перпендикулярно ее плоскости, поэтому угол между дверью и направлением силы был \(90\) градусов.

Так как
\(\tau = r \times F = r F \sin (\theta)\) 

Диаграмма примера задачи

, то крутящий момент на двери был:
\(\tau = (1,0 м) (50 Н ) \sin(90)\)
\(\tau = 50 Н·м\)

Обратите внимание, что это только величина крутящего момента; чтобы завершить ответ, нам нужно найти направление крутящего момента. Используя правило правой руки , мы видим, что направление крутящего момента выходит за пределы экрана.

Что такое крутящий момент? Все о крутящем моменте: определение, уравнения и единицы измерения

Советы и рекомендации

• Главная страница
• Характеристики
• Советы и рекомендации

Часто сравнивают значения крутящего момента двигателя, но что такое крутящий момент и почему он важен?

Автор: Auto Express

16 декабря 2020 г.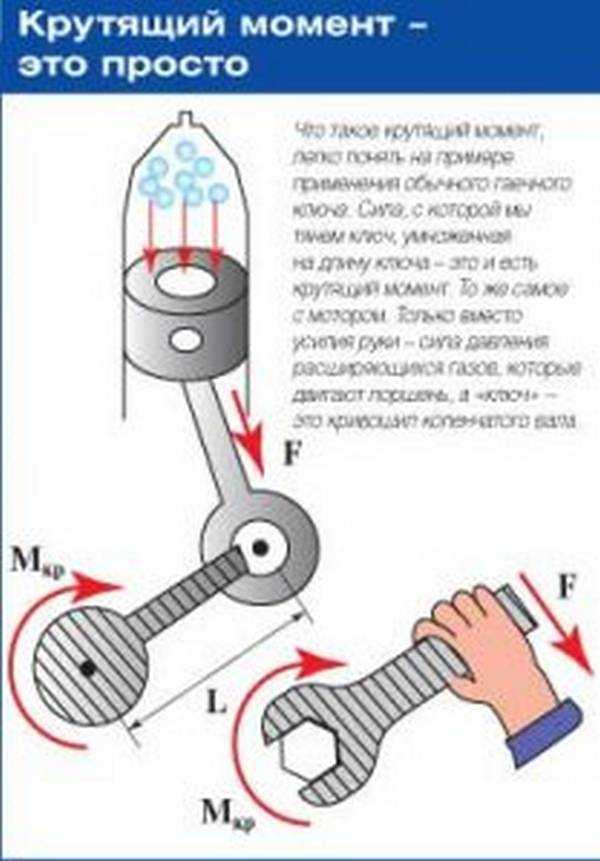

16 декабря 2020 г.

Крутящий момент — это слово, которое широко используется производителями автомобилей, рекламодателями и рецензентами, и оно так же важно, как и другие заголовки, которые вы увидите. через suce как лошадиные силы. Однако реклама крутящего момента не всегда была чем-то само собой разумеющимся — оглянитесь назад на рекламу автомобилей 19-го века.80-х, и вы обнаружите, что это почти никогда не упоминается.

В основном из-за лишнего веса новых автомобилей. Современные моторы настолько перегружены технологиями, комфортом и безопасностью, что весят намного больше, чем их аналоги десятилетней давности. Это означает, что этим автомобилям требуется больше силы или крутящего момента, чтобы заставить их двигаться.

Крутящий момент определяется как сила вращения двигателя. Вы можете заметить, что крутящий момент, как и лошадиные силы, всегда выражается при определенной частоте вращения двигателя. Например, Ford Fiesta Ecoboost развивает максимальный крутящий момент в диапазоне от 1400 до 4000 об/мин. Вообще говоря, автомобиль будет чувствовать себя более отзывчивым, когда пиковый крутящий момент развивается в нижнем диапазоне оборотов, но многим людям нравятся мощные двигатели, которые необходимо сильно раскручивать, прежде чем они развивают пиковый крутящий момент.

Крутящий момент становится все более важным, поскольку автомобили становятся больше и тяжелее. Крошечный городской автомобиль может легко двигаться с очень небольшим крутящим моментом, в то время как большому внедорожнику или фургону требуется много времени, чтобы заставить его двигаться. Вот почему более крупные автомобили, как правило, оснащаются дизельными двигателями — дизели развивают больший крутящий момент при более низких оборотах, чем бензиновые двигатели.

Что такое крутящий момент?

Проще говоря, определение крутящего момента — это сила вращения двигателя. Он отличается от лошадиных сил, поскольку относится к объему работы, которую может выполнить двигатель, а мощность определяет, насколько быстро эта работа может быть выполнена.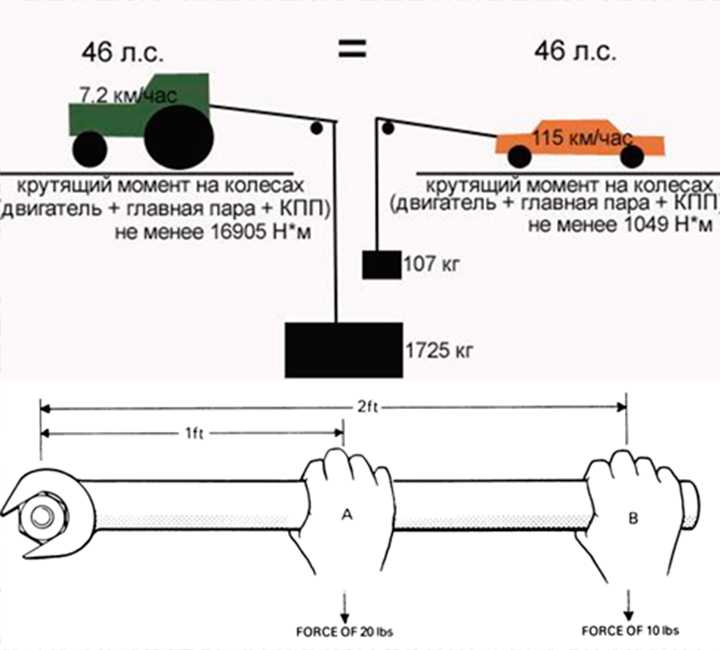 Вот почему крутящий момент часто называют неспециалистами «тяговой силой», «мощностью» или «ворчанием».

Крутящий момент обычно измеряется в ньютон-метрах (Нм) или фунт-футах (фунт-фут) – последнее не следует путать с фут-фунтом (фут-фунт), поскольку один фут-фунт относится не к крутящей силе, а к количеству энергии, необходимой для подъема груза массой 1 фунт на расстояние 1 фут.

В частности, крутящий момент фактически измеряет силу, необходимую для скручивания объекта (например, при затягивании крышки на бутылке с газировкой, колесной гайки или болта головки цилиндра). Или, в случае двигателя, он измеряет, какое крутящее усилие доступно на коленчатом валу при любых заданных оборотах двигателя (об/мин).

• Автомобили категорий D и C: объяснение списания по страховке

В автомобиле мощность – это мера того, насколько быстро двигатель может развить один и тот же крутящий момент с течением времени, поэтому быстрее вы можете ускориться. Одна лошадиная сила (HP) — это совершенно произвольная единица, придуманная инженером Джеймсом Уаттом. Это эквивалентно тому, что одна лошадь поднимает вес в 33 000 фунтов на высоту в двенадцать дюймов за одну минуту — или 33 000 футо-фунтов в минуту. Метрический эквивалент (PS) равен 4500 кг-м в минуту, или 0,97 л.с.

Тормозная мощность (BHP) немного ниже, чем HP, но, возможно, является более точным показателем, поскольку учитывает потери мощности на внутреннее трение двигателя.

Основные уравнения крутящего момента

Предположим, мы используем ключ длиной 0,5 м для затягивания колесной гайки, и нам нужно опереться на дальний конец ключа с усилием 50 ньютонов, чтобы затянуть ее. Простое умножение двух чисел дает требуемый показатель крутящего момента в ньютон-метрах:

50 (Н) x 0,5 (м) x = 25 Нм крутящего момента

Если вы хотите сохранить старую школу, вы можете измерять расстояние в футах и ​​силу в фунтах. На этот раз наш ключ может быть 18 дюймов (1½ фута), и мы прикладываем усилие 20 фунтов к дальнему концу: 

20 (фунтов) x 1½ (футов) = 30 фунт-футов крутящего момента крутящий момент выглядит?

Если двигатель развивает крутящий момент 500 Нм, мы можем использовать аналогичную визуализацию в обратном направлении, чтобы лучше понять задействованные силы. Чтобы остановить вращение такого двигателя, потребуется гаечный ключ длиной один метр, прикрепленный к коленчатому валу, с усилием в 500 ньютонов на другом конце. Так как один килограмм действует с силой примерно в 90,8 ньютона в гравитации Земли, это означает, что вам понадобится 50-килограммовый жокей, чтобы стоять на конце. Или Аллан Макниш.

• Автомобильные часы: законна ли корректировка пробега?

Если это не кажется большим усилием, чтобы остановить двигатель, развивающий внушительные 500 Нм, не забывайте, что крутящий момент на колесах значительно увеличивается при снижении оборотов двигателя. Таким образом, жокей мог остановить двигатель, но он не мог остановить машину!

Что лучше, крутящий момент или мощность?

Крутящий момент и мощность очень тесно связаны, потому что в двигателе внутреннего сгорания одно не может быть без другого. Снова математика, так как HP рассчитывается следующим образом: 

л.с. = крутящий момент x об/мин ÷ 5252

Это означает, что если сравнить два двигателя с разным крутящим моментом, то двигатель с более высоким крутящим моментом всегда будет иметь большую мощность при любой заданной частоте вращения двигателя.