Таблица дифференциал: III Таблица дифференциалов

III Таблица дифференциалов

Так как дифференциал dyлишь множителемdxотличается от производной,
то по таблице производных легко составить
таблицу дифференциалов.

1.
,,.

2.
,.

3.
,.

4.
. 5..

6.
. 7..

8.
. 9..

10.
. 11..

Также легко получить формулы для
дифференциалов суммы, разности,
произведения и частного функций:

а)

б)

в)

Отметим, что в таблице дифференциалов
переменная xможет быть как независимой, так и
некоторой функцией. В таблице же
производных (§6)x– это только независимая переменная.

Замечание.Формула для дифференциала
функции,
а именно:

,

позволяет написать формулу, выражающую
производную функции через дифференциалы
dxиdy:

.

При этом такая формула сохраняет силу,
по какой бы независимой переменной ни
были вычислены dxиdy.
Эта формула позволяет легко запоминать
(но не доказывать!) некоторые правила
дифференцирования:

для сложной функции

;

для обратной функции

;

для функции, заданной параметрически

.

§8. Производные высших порядков

I Определение и обозначения

Если функция
дифференцируема на некотором промежутке,
то её производнаясама является функцией, определенной
на этом промежутке. Следовательно, по
отношению к ней можно ставить вопрос о
существовании и нахождении производной.
Если она существует, то её называют
второй производной (или производной
2^гопорядка), и обозначают одним
из символов

.

Аналогично, если существует производная
от второй производной, то её называют
третьей производной и обозначают,
например,
.

Вообще, производной n-го
порядка называют производную от
производной (n–1)-го
порядка и обозначают.
Итак, по определению

.

II Производные некоторых функций

1. y=sinx,
y=cosx

Первые производные этих функций
и формулы приведенияпозволяют методом математической
индукции получить выражения для
производныхn-го
порядка:

.

2.
y=x^

Если
,
то, последовательно дифференцируя,
получим,,
и вообще:

.

Если же показатель степени натуральный,
то:

3. y=a^x

,
в частности,,.

4. y=lnx

,

.

III Некоторые правила

Очевидно, что
и.
Для производной

n-го
порядка от произведения функций имеется
т.н. формула Лейбница. Приведем ее без
доказательства:

,
где.

Заметим, что под производной нулевого
порядка принято понимать саму

функцию:
.

IV Функция,
заданная параметрически

Пусть функция задана параметрическими
уравнениями

Её первая производная – это также
функция, заданная параметрически:

Тогда

Пример. Дляпервая производная имеет видТогдаи вторая производная такова:

V Функция,
заданная неявно

Повторное дифференцирование такой
функции покажем на примере:

Тогда по определению:

.

Остается подставить в последнее выражение
значение
:

.

Полученное выражение можно упростить,
используя само уравнение:

.

Тема
ОСНОВНЫЕ
ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ

Лекция 10

§1. Необходимое
условие экстремума

Рассмотрим функцию
,
определенную на промежутке,
и пусть точка–внутренняяточка промежутка:.

Определение 1.Точканазывается точкой (локального) максимума
функции,
если существует окрестность этой точки,
в которой (при)
выполняется неравенство.
Другими словами для малых приращений
аргументаприращение
функции.

Определение 2.Точканазывается точкой (локального) минимума
функции,
если существует окрестность этой точки,
в которой (при)
выполняется неравенство.
Другими словамипри малых.

Точки максимума и минимума называются
точками экстремума. Их можно характеризовать
следующим образом: приращение функции
в точке экстремума имеет постоянный
знак, не зависящий от знака
(еслидостаточно мало).

Теорема Ферма.Если функциядифференцируема в точкеи имеет в этой точке локальный экстремум,
то.

Доказательство.Дифференцируемость
означает существование конечного
предела

.

Для этого предела имеется три возможности:
1)
;
2);

3)
.
Предположим, что.
Тогда для близких к нулюразностное отношение.
Если же,
то и(для малых).
В обоих случаях знакзависит от знака.
Но по условию теоремы– это точка экстремума, значит, знакне зависит от знака.
Это противоречие означает, чтоне может быть ни положительным, ни
отрицательным.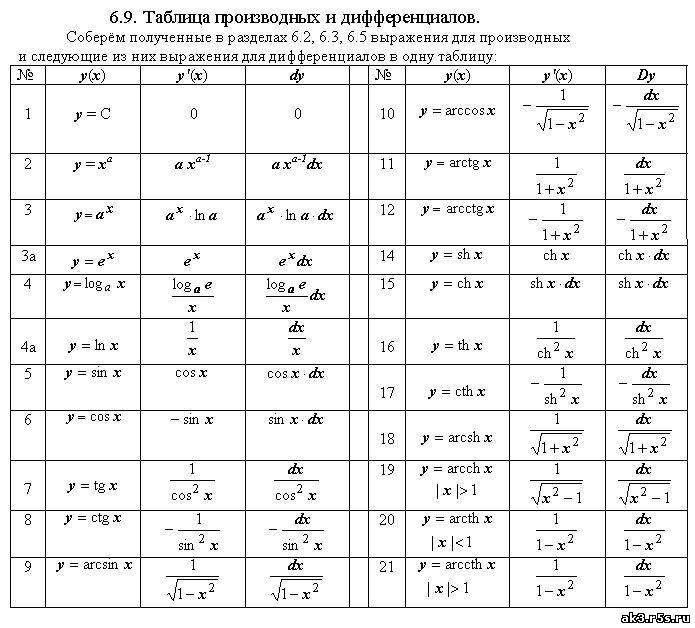 Остается последняя
возможность:.

Замечание 1.Эта теорема имеет
простой геометрический смысл: если в
точке графика функции,
которой соответствует экстремум функции,
существует касательная к графику, то
эта касательная параллельная осиOx.

Замечание 2.Сформулированное
в теореме условиеявляется необходимым, но не достаточным.
Например, функцияимеет производную,
которая обращается в ноль в точке.
Однако,

.

Выражение в скобках всегда положительно,
как неполный квадрат суммы. Следовательно,

и в точкенет экстремума.

Дифференциал онлайн

dy=f′(x)dx

Как видим, для нахождения дифференциала нужно умножить производную на dx. Это позволяет из таблицы формул для производных сразу записать соответствующую таблицу для дифференциалов.

Полный дифференциал для функции двух переменных:

Полный дифференциал для функции трех переменных равен сумме частных дифференциалов: d f(x,y,z)=dxf(x,y,z)dx+dyf(x,y,z)dy+dzf(x,y,z)dz

• Решение онлайн
• Видеоинструкция
• Также решают

f(x) =

Примеры

≡ x^2/(x+2)
cos2(2x+π) ≡ (cos(2*x+pi))^2
≡ x+(x-1)^(2/3)

Вместе с этим калькулятором также используют следующие:

Точки разрыва функции

Решение пределов:

Построение графика функции методом дифференциального исчисления

Экстремум функции двух переменных

Вычисление интегралов

см. также Вычисление приближенно с помощью дифференциала

Определение. Функция y=f(x) называется дифференцируемой в точке x₀, если ее приращение в этой точке можно представить в виде ∆y=A∆x + α(∆x)∆x, где A – константа, а α(∆x) – бесконечно малая при ∆x → 0.

Требование дифференцируемости функции в точке эквивалентно существованию производной в этой точке, причем A=f’(x₀).

Пусть f(x) дифференцируема в точке x₀ и f ‘(x₀)≠0, тогда ∆y=f’(x₀)∆x + α∆x, где α= α(∆x) →0 при ∆x→0. Величина ∆y и каждое слагаемое правой части являются бесконечно малыми величинами при ∆x→0. Сравним их: , то есть α(∆x)∆x – бесконечно малая более высокого порядка, чем f’(x₀)∆x.

то есть ∆y~f’(x₀)∆x. Следовательно, f’(x₀)∆x представляет собой главную и вместе с тем линейную относительно ∆x часть приращения ∆y (линейная – значит содержащая ∆x в первой степени). Это слагаемое называют дифференциалом функции y=f(x) в точке x₀ и обозначают dy(x₀) или df(x₀). Итак, для произвольных значений x
dy=f′(x)∆x. (1)

Полагают dx=∆x, тогда

dy=f′(x)dx. (2)

Пример. Найти производные и дифференциалы данных функций.

а) y=4tg2x

Решение:

дифференциал:
б)
Решение:

дифференциал:
в) y=arcsin2(lnx)

Решение:

дифференциал:
г)
Решение:

=
дифференциал:

Пример. Для функции y=x³ найти выражение для ∆y и dy при некоторых значениях x и ∆x.

Решение. ∆y = (x+∆x)³ – x³ = x³ + 3x²∆x +3x∆x² + ∆x³ – x³ = 3x²∆x+3x∆x²+∆x³; dy=3x²∆x (взяли главную линейную относительно ∆x часть ∆y). В данном случае α(∆x)∆x = 3x∆x² + ∆x³.

Таблица производных

Таблица производных