Содержание
Автомобильные дифференциалы
Каталог
Дифференциал — его назначение и устройство.
При движении автомобиля крутящий момент от коленвала двигателя передается коробке передач и затем, через главную передачу и дифференциал, на ведущие колеса. Главная передача позволяет увеличивать или уменьшать крутящий момент передаваемый колесам автомобиля и одновременно уменьшать и соответственно увеличивать скорость вращения колес. Передаточное число в главной передаче подбирается таким образом, что максимальный крутящий момент и частота вращения ведущих колес находятся в наиболее оптимальных значениях для конкретного автомобиля. Кроме того, главная передача очень часто является объектом тюнинга автомобиля.
Главная передача автомобиля — это не что иное, как шестеренчатый понижающий редуктор, в котором ведущая шестерня связана с вторичным валом КПП, а ведомая – с колесами автомобиля. По типу зубчатого соединения главные передачи различаются на следующие разновидности:
- цилиндрическая – в большинстве случаев применяется на автомобилях с поперечным расположением двигателя и коробки передач и передним приводом;
- коническая – применяется очень редко, так как имеет большие габариты и высокий уровень шума;
- гипоидная – наиболее востребованная разновидность главной передачи, которая применяется на большинстве автомобилей с классическим задним приводом.
 Гипоидная передача отличается малыми размерами и низким уровнем шума;
Гипоидная передача отличается малыми размерами и низким уровнем шума; - червячная – практически не применяется на автомобилях по причине трудоемкости изготовления и высокой стоимости.
Также стоит отметить, что автомобили с передним и задним приводом имеют различное расположение главной передачи. В переднеприводных автомобилях с поперечным расположением КПП и силового агрегата, цилиндрическая главная передача располагается непосредственно в картере КПП. В автомобилях с классическим задним приводом главная передача установлена в корпусе ведущего моста и соединена с коробкой передач посредством карданного вала. В функционал гипоидной передачи заднеприводного автомобиля также входит и разворот вращения на 90 градусов за счет конических шестерен. Несмотря на различные типы и расположение, предназначение главной передачи остается неизменным.
Дифференциал автомобиля чаще всего совмещен с главной передачей и располагается соответственно в картере коробки передач или в корпусе заднего моста.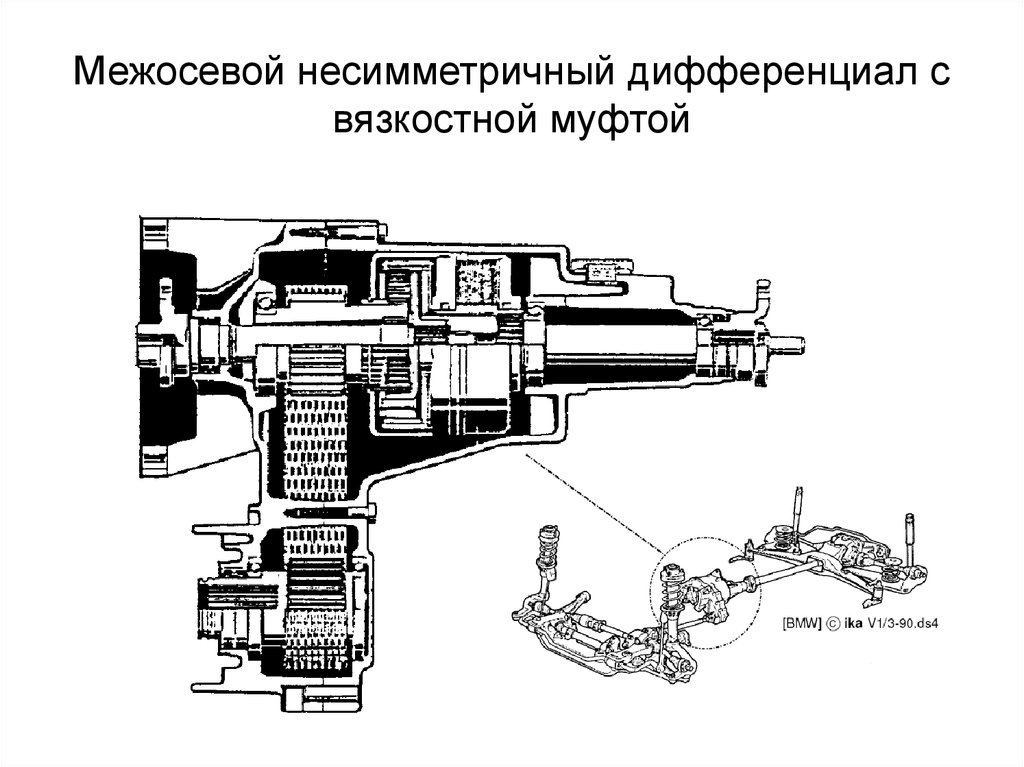 Однако дифференциал может быть установлен и между ведущими осями полноприводного автомобиля. Дифференциал представляет собой планетарный редуктор и делится на следующие разновидности:
Однако дифференциал может быть установлен и между ведущими осями полноприводного автомобиля. Дифференциал представляет собой планетарный редуктор и делится на следующие разновидности:
- конический – в большинстве случаев устанавливается совместно с главной передачей между колесами одной приводной оси;
- цилиндрический – наиболее часто применяется для развязки ведущих осей полноприводных автомобилей;
- червячный – является универсальным и устанавливается как между колесами, так и между ведущими осями.
Основное предназначение дифференциала заключается в распределении крутящего момента между колесами автомобиля и изменения их частоты вращении относительно друг друга. Так, например поворот автомобиля без дифференциала был бы попросту невозможен, так как при повороте внешнее колесо обязательно должно вращаться с большей частотой, нежели внутреннее. Дифференциалы существуют симметричные и несимметричные. Симметричный дифференциал передает равный крутящий момент на оба колеса и устанавливается чаще всего совместно с главной передачей.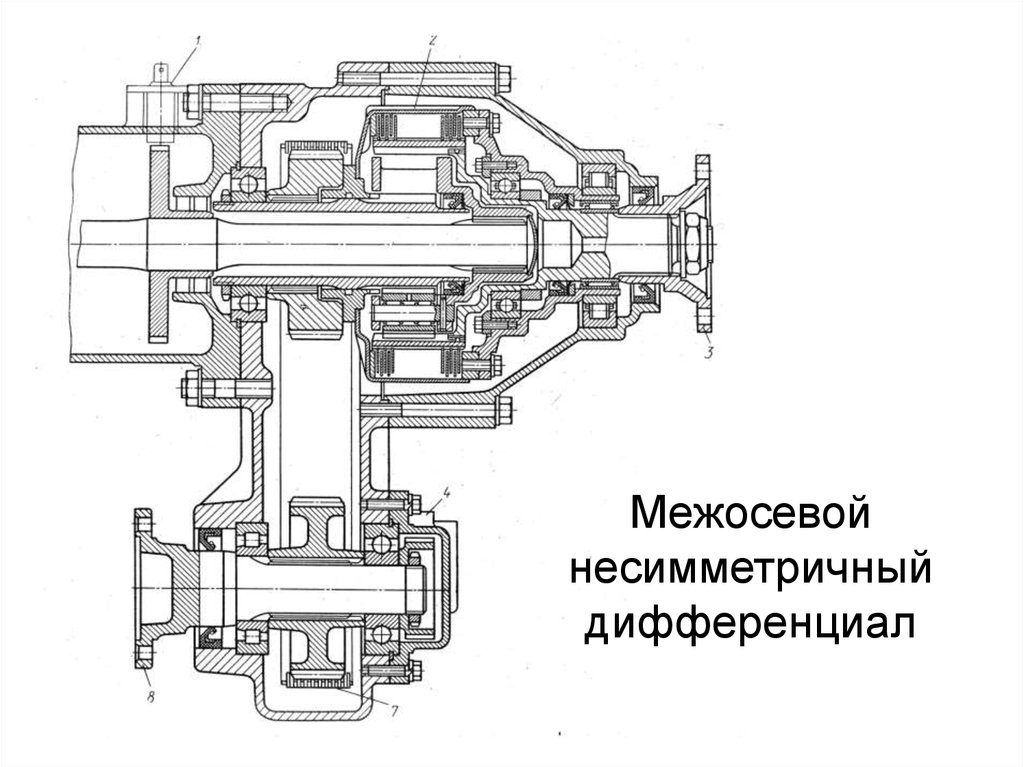 Несимметричный дифференциал позволяет передать крутящий момент в различных пропорциях и устанавливается между приводными осями автомобиля.
Несимметричный дифференциал позволяет передать крутящий момент в различных пропорциях и устанавливается между приводными осями автомобиля.
Дифференциал состоит из корпуса, шестерен сателлитов и полуосевых шестерен. Корпус обычно совмещен с ведомой шестерней главной передачи. Шестерни сателлиты играют роль планетарного редуктора и соединяют полуосевые шестерни с корпусом дифференциала. Полуосевые (солнечные) шестерни соединены с ведущими колесами посредством полуосей на шлицевых соединениях. При всех плюсах у простейшего дифференциала существует и недостаток. Дело в том, что частота вращения может быть распределена на колеса не только в соотношении, например 50/50, 40/60 или 35/65, но и 0/100. То есть, на одно колесо автомобиля может быть передан абсолютно весь крутящий момент, в то время как второе колесо будет абсолютно статично. Такое случается в том случае если автомобиль застрял в грязи или на льду.
Однако современные дифференциалы более совершенны и практически лишены данного недостатка. Многие дифференциалы имеют жесткую автоматическую или ручную блокировку. Кроме того современные легковые полноприводные автомобили снабжаются системой курсовой устойчивости, которая основана на оптимальном распределении крутящего момента между осями и отдельными колесами в зависимости от траектории движения.
Многие дифференциалы имеют жесткую автоматическую или ручную блокировку. Кроме того современные легковые полноприводные автомобили снабжаются системой курсовой устойчивости, которая основана на оптимальном распределении крутящего момента между осями и отдельными колесами в зависимости от траектории движения.
Уважаемые посетители сайта!
Если Вы не нашли у нас то, что искали — не уходите сразу.
Обратите внимание на большой ассортимент предлагаемых товаров: электроинструмент, тепловое и насосное оборудование Quattro Elementi, расходные материалы Практика, автоинструмент Forsage, наборы инструмента KingTul (самые дешевые в РФ). А так-же компрессорное, сварочное оборудование, ручной инструмент и комплектующие. У нас есть товары для дачников и садоводов, для автолюбителей и фермеров, для ремонта или строительства.
Наш интернет-магазин предложит отличную цену в Санкт-Петербурге, и доставку в другие города. Для оптовых покупателей предоставляем отсрочку платежа, доставку товара и другие необходимые условия сотрудничества. Выберите на сайте что-то необходимое и мы будем рады продать Вам этот товар по отличной цене.
Выберите на сайте что-то необходимое и мы будем рады продать Вам этот товар по отличной цене.
Распределение крутящих моментов между осями несимметричного дифференциала
Распределение крутящих моментов между осями (3) [рис. 1, в)] несимметричного дифференциала осуществляется по следующей схеме. В дифференциале имеются двойные конические сателлиты (4). Через шестерню (2) они соединяются с его передней осью, а через шестерню (12) – с задней.
Рис. 1. Схемы дифференциалов.
а) – Схема симметричного блокируемого дифференциала;
б) – Схема симметричного самоблокирующегося дифференциала;
в) – Схема несимметричного дифференциала:
1) – Ведущая шестерня;
2) – Коническая шестерня дифференциала;
3) – Полуось;
4) – Сателлит;
5) – Ведомая шестерня;
6) – Корпус дифференциала;
7) – Крестовина;
8) – Зубцы корпуса;
9) – Зубчатая муфта;
10) – Ведущие диски;
11) – Ведомые диски;
12) – Коническая шестерня дифференциала;
13) – Нажимные чашки.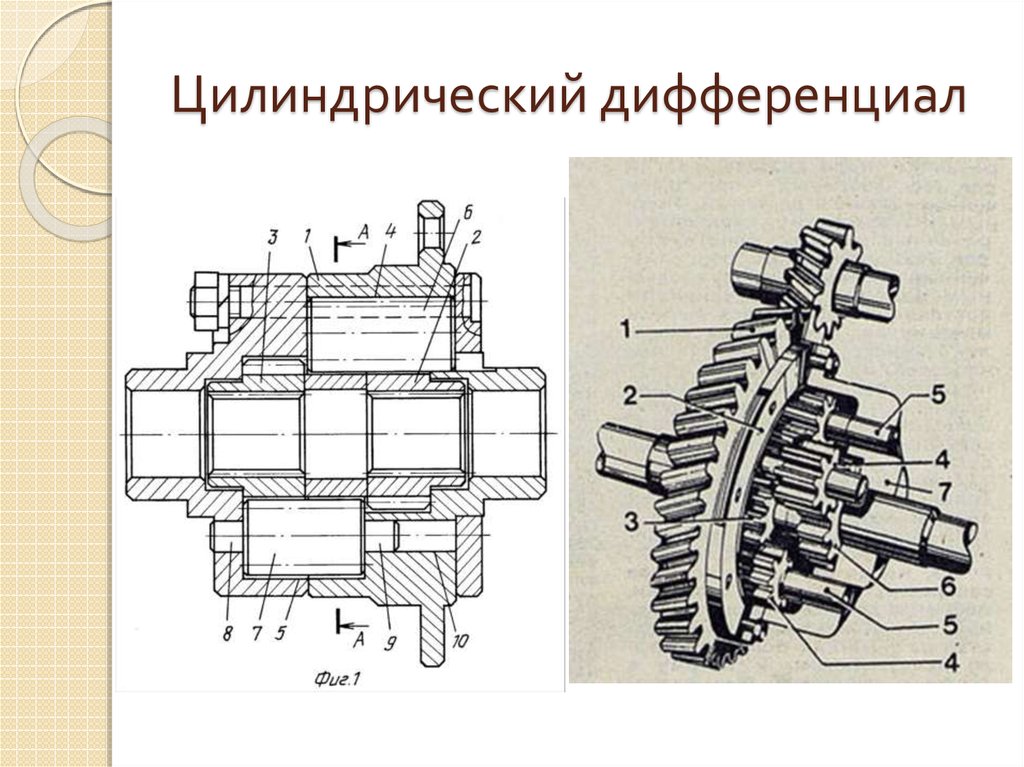
Из условия равновесия блока сателлитов относительно его оси P1r1=P1r1 либо
P2/P1=r1/r2
* где P1 и r1 – окружное усилие и радиус начальной скорости большего сателлита соответственно, P2 и r2 – то же меньшего сателлита.
Крутящие моменты Мдиф.1 и Мдиф.2, передаваемые передней и задней осям дифференциала соответственно
Мдиф.1=P1R1
Мдиф.2=P2R2
* где R1 и R2 – радиусы начальных окружностей осевых шестерён (2) и (12).
Разделив уравнение (Мдиф.2=P2R2) на уравнение (Мдиф.1=P1R1) с учётом уравнения (P2/P1=r1/r2), получаем
Мдиф.2/Мдиф. 1=(r1/r2)•(R2/R1)=iд
1=(r1/r2)•(R2/R1)=iд
* где iд – передаточное число дифференциала.
Мдиф.1+Мдиф.2=Мдиф
* где Мдиф – крутящий момент, подводимый к корпусу дифференциала.
Решая совместно уравнения (Мдиф.2/Мдиф.1=(r1/r2)•(R2/R1)=iд) и (Мдиф.1+Мдиф.2=Мдиф), получаем
Мдиф.1=Мдиф/(1+iд)
Мдиф.2=Мдифiд/(1+iд)
Таким образом, распределение крутящих моментов между осями при несимметричном дифференциале зависит от значения передаточного числа дифференциала (iд). В частном случае, когда r1=r2 и R1=R2 (симметричный дифференциал), iд=1 и Мдиф.1=Мдиф.2.
Симметричный межосевой дифференциал используется в тех случаях, когда сцепные веса обоих ведущих осей одинаковы. В противном случае применяется дифференциал несимметричного типа.
В противном случае применяется дифференциал несимметричного типа.
17*
Существование значения для дифференциальной игры с асимметричной информацией и выявлением сигналов
Aumann RJ, Maschler MB (1995) Повторные игры с неполной информацией. В сотрудничестве с Ричардом Э. Стернсом. MIT Press, Кембридж
Google ученый
Барди М., Капуццо-Дольчетта И. (1996) Оптимальное управление и вязкостные решения уравнений Гамильтона-Якоби-Беллмана. Биркхойзер, Базель
Google ученый
Бернхард П., Рапапорт А. (1995) Этюд игры на самолете с неверным знанием координат. Automatique-productique Industrielle Industrielle 29:575–601
Google ученый
Buckdahn R, Cardaliaguet P, Quincampoix M (2011) Некоторые последние аспекты дифференциальной теории игр. Приложение Dyn Games 1(1):74–114
Статья
Google ученый
Buckdahn R, Li J, Quincampoix M (2013) Функция ценности дифференциальных игр без условий Айзекса. подход с неупреждающими смешанными стратегиями. Int J Game Theory 42(4):989–1020
подход с неупреждающими смешанными стратегиями. Int J Game Theory 42(4):989–1020
Статья
Google ученый
Buckdahn R, Quincampoix M, Rainer C, Xu Y (2015) Дифференциальные игры с асимметричной информацией и без условия Айзекса. Int J Теория игр. https://doi.org/10.1007/s00182-015-0482-x
Артикул
Google ученый
Cardaliaguet P (2007) Дифференциальные игры с асимметричной информацией. SIAM J Control Optim 46(3):816–838
Статья
Google ученый
Cardaliaguet P (2009) Проблема двойного препятствия, возникающая в теории дифференциальных игр. J Math Anal Appl 360(1):95–107
Статья
Google ученый
Cardaliaguet P (2010) Введение в дифференциальные игры. Конспект лекций. Université de Bretagne Occidentale, Брест
Google ученый
Cardaliaguet P, Jimenez C, Quincampoix M (2014) Чистые и случайные стратегии в дифференциальной игре с неполной информацией. J Dyn Games 1(3):363–375
J Dyn Games 1(3):363–375
Статья
Google ученый
Cardaliaguet P, Quincampoix M (2008) Детерминированные дифференциальные игры при вероятностном знании начального состояния. Int Game Theory Rev 10(01):1–16
Артикул
Google ученый
Cardaliaguet P, Rainer C (2009) Об игре с непрерывным временем с неполной информацией. Math Oper Res 34(4):769–794
Статья
Google ученый
Cardaliaguet P, Rainer C (2009) Стохастические дифференциальные игры с асимметричной информацией. Appl Math Optim 59(1):1–36
Статья
Google ученый
Cardaliaguet P, Rainer C (2012) Игры с неполной информацией в непрерывном времени и для непрерывных типов. Приложение Dyn Games 2(2):206–227
Статья
Google ученый
Cardaliaguet P, Rainer C (2013) Стратегии путей для стохастических дифференциальных игр с исправлением «стохастических дифференциальных игр с асимметричной информацией». Appl Math Optim 68(1):75–84
Appl Math Optim 68(1):75–84
Статья
Google ученый
Crandall M, Ishii H, Lions PL (1992) Руководство пользователя по вязкостным решениям уравнений в частных производных второго порядка. Bull Am Soc 27:1–67
Статья
Google ученый
Crandall M, Lions PL (1983) Вязкостные решения уравнений Гамильтона-Якоби. Trans Am Math Soc 277:1–42
Статья
Google ученый
Де Мейер Б (1996) Повторные игры, двойственность и центральная предельная теорема. Math Oper Res 21(1):237–251
Статья
Google ученый
Докнер Э.Дж., Йоргенсен С., Лонг Н.В., Зоргер Г. (2000) Дифференциальные игры в экономике и науке управления. Издательство Кембриджского университета, Кембридж
Книга
Google ученый
Эллиотт Р. Дж., Калтон Н.Дж. (1972) Существование ценности в дифференциальных играх преследования и уклонения. J Различное уравнение 12(3):504–523
Дж., Калтон Н.Дж. (1972) Существование ценности в дифференциальных играх преследования и уклонения. J Различное уравнение 12(3):504–523
Артикул
Google ученый
Evans LC, Souganidis PE (1984) Дифференциальные игры и формулы представления решений уравнений Гамильтона-Якоби-Айзекса. Математический университет Индианы J 33 (5): 773–797
Статья
Google ученый
Fershtman C, Nitzan S (1991) Динамичное добровольное предоставление общественных благ. Eur Econ Rev 35(5):1057–1067
Статья
Google ученый
Forges F (1982) Бесконечно повторяющиеся игры с неполной информацией: симметричный случай со случайными сигналами. Int J Game Theory 11: 203–213
Статья
Google ученый
Исаакс Р. (1967) Дифференциальные игры. Уайли, Нью-Йорк
Google ученый
Jimenez C, Quincampoix M (2018) Уравнения Гамильтона Якоби Айзекса для дифференциальных игр с асимметричной информацией о вероятностных начальных условиях.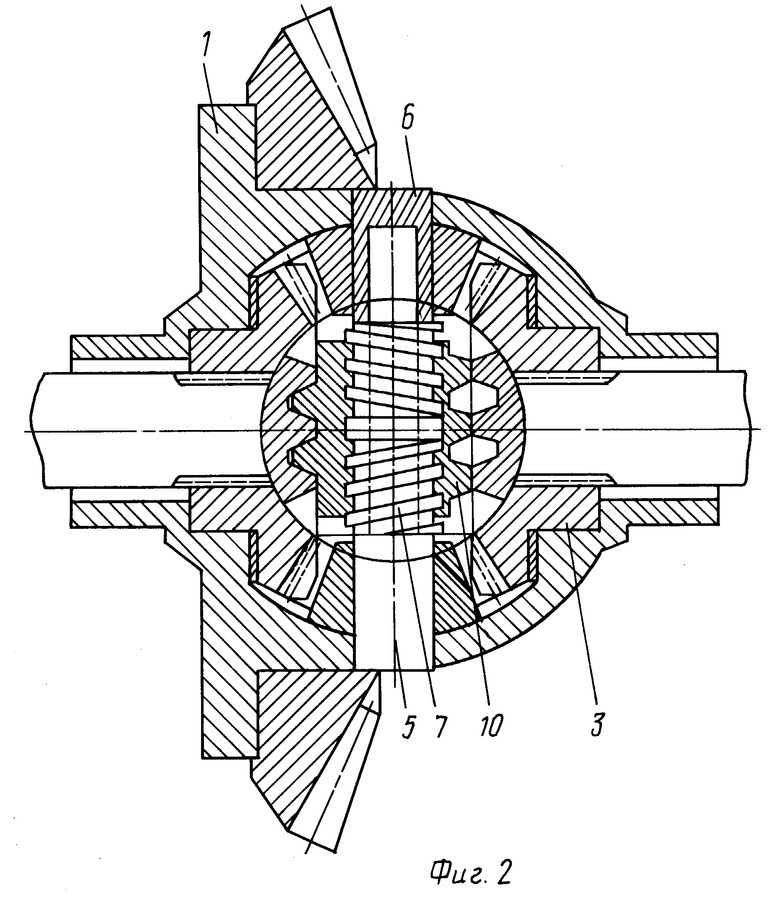 J Math Anal Appl 457 (2): 1442–1451
J Math Anal Appl 457 (2): 1442–1451
Артикул
Google ученый
Хименес С., Кенкампуа М., Сюй Ю. (2014) Дифференциальные игры с неполной информацией о континууме начальных позиций и без условия Айзекса. Приложение Dyn Games 6:1–15
Google ученый
Мертенс Дж., Замир С. (1976) О повторяющихся играх без рекурсивной структуры. Int J Game Theory 5:173–182
Статья
Google ученый
Нейман А., Сорин С. (1997) Равновесия в повторяющихся играх с неполной информацией: детерминированный симметричный случай. В: Parthasaraty T (ed) Применение теории игр к исследованию экономики и операций. Спрингер, Бостон
Google ученый
Нейман А., Сорин С. (1998) Равновесия в повторяющихся играх с неполной информацией: общий симметричный случай. Int J Game Theory 27: 201–210
Статья
Google ученый
Олиу-Бартон М.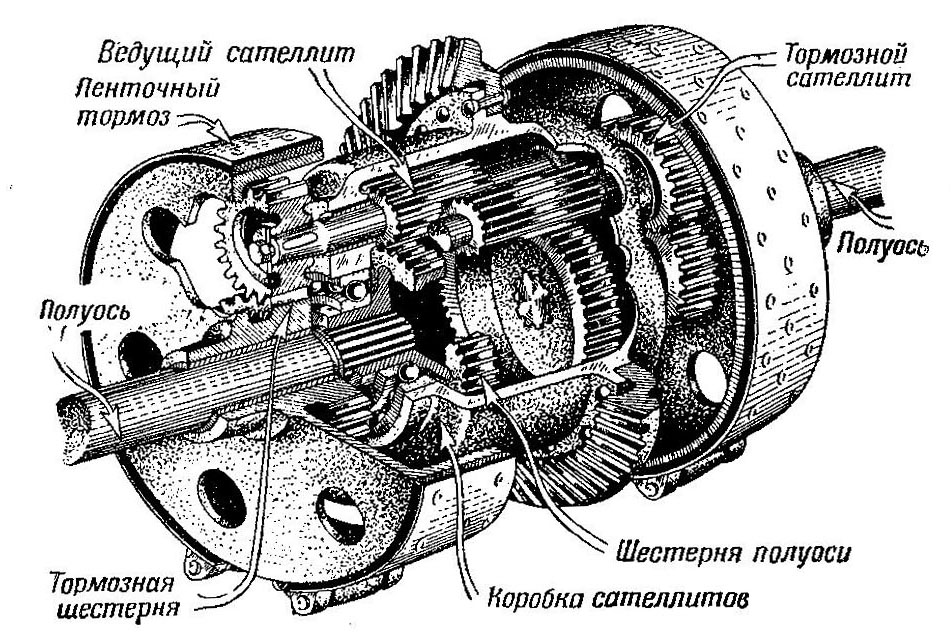 (2015) Дифференциальные игры с асимметричной и коррелированной информацией. Приложение Dyn Games 5(3):378–396
(2015) Дифференциальные игры с асимметричной и коррелированной информацией. Приложение Dyn Games 5(3):378–396
Статья
Google ученый
Roxin E (1969) Аксиоматический подход в дифференциальных играх. J Optim Theory Appl 3(3):153–163
Статья
Google ученый
Сорин С (1980) О повторяющихся играх без рекурсивной структуры: существование Lim \(V_n\). Int J Теория игр 9(4):201–215
Google ученый
Сорин С (2002) Первый курс по повторяющимся играм с нулевой суммой. Спрингер, Нью-Йорк
Google ученый
Варайя П., Лин Дж. (1969) Существование седловых точек в дифференциальных играх. SIAM J Control 7(1):141–157
Статья
Google ученый
Waternaux C (1983) Решение для класса повторяющихся игр без рекурсивной структуры. Int J Game Theory 12: 129–160
Int J Game Theory 12: 129–160
Статья
Google ученый
Wu X (2017) Существование значения для дифференциальных игр с неполной информацией и сигналами о начальных состояниях и выигрышах. J Math Anal Appl 446(2):1196–1218
Статья
Google ученый
Wu X (2018) Существование значения для дифференциальной игры с неполной информацией и выявлением. SIAM J Control Optim 56(4):2536–2562
Артикул
Google ученый
Wu X (2019) Дифференциальные игры с бесконечным горизонтом с асимметричной информацией. Приложение Dyn Games 9:858–880
Статья
Google ученый
Wu X (2021) Дифференциальные игры с неполной информацией и с выявлением сигнала: симметричный случай. Приложение Дин Игры. https://doi.org/10.1007/s13235-021-00376-1
Статья
Google ученый
Доминирующие факторы электромагнитных помех проблемы несимметричных и равноудаленных дифференциально-парных линий
Доминирующие факторы проблем электромагнитных помех несимметричных и равноудаленных дифференциально-парных линий
- Каяно, Йошики
- Иноуэ, Хироси
;
Аннотация
Многоканальная схема дифференциальной сигнализации является одной из ключевых технологий для современных электронных систем. Для реальной системы невозможно установить идеальный баланс или симметричную топологию, и, следовательно, возбуждается компонент дисбаланса. Чтобы представить основные соображения относительно электромагнитного (ЭМ) излучения от практической структуры асимметричных дифференциально-парных линий с равноудаленной трассировкой, в которой парные линии одинаковой длины используются в макете высокоскоростной платы/БИС, в этой статье мы впервые попытка уточнить характеристики и определить доминирующий дисбаланс и фактор электромагнитного излучения от асимметричных дифференциально-парных линий с помощью модели, основанной на физике. Частотная характеристика ЭМ-излучения асимметричных дифференциально-парных линий может быть определена с помощью физической модели. Физическая модель построена с использованием модели эквивалентной схемы для расчета распределения тока и модели излучения на основе дипольной антенны Герца. Это подтверждается путем сравнения предсказанных результатов с моделированием во временной области с конечной разностью.
Для реальной системы невозможно установить идеальный баланс или симметричную топологию, и, следовательно, возбуждается компонент дисбаланса. Чтобы представить основные соображения относительно электромагнитного (ЭМ) излучения от практической структуры асимметричных дифференциально-парных линий с равноудаленной трассировкой, в которой парные линии одинаковой длины используются в макете высокоскоростной платы/БИС, в этой статье мы впервые попытка уточнить характеристики и определить доминирующий дисбаланс и фактор электромагнитного излучения от асимметричных дифференциально-парных линий с помощью модели, основанной на физике. Частотная характеристика ЭМ-излучения асимметричных дифференциально-парных линий может быть определена с помощью физической модели. Физическая модель построена с использованием модели эквивалентной схемы для расчета распределения тока и модели излучения на основе дипольной антенны Герца. Это подтверждается путем сравнения предсказанных результатов с моделированием во временной области с конечной разностью.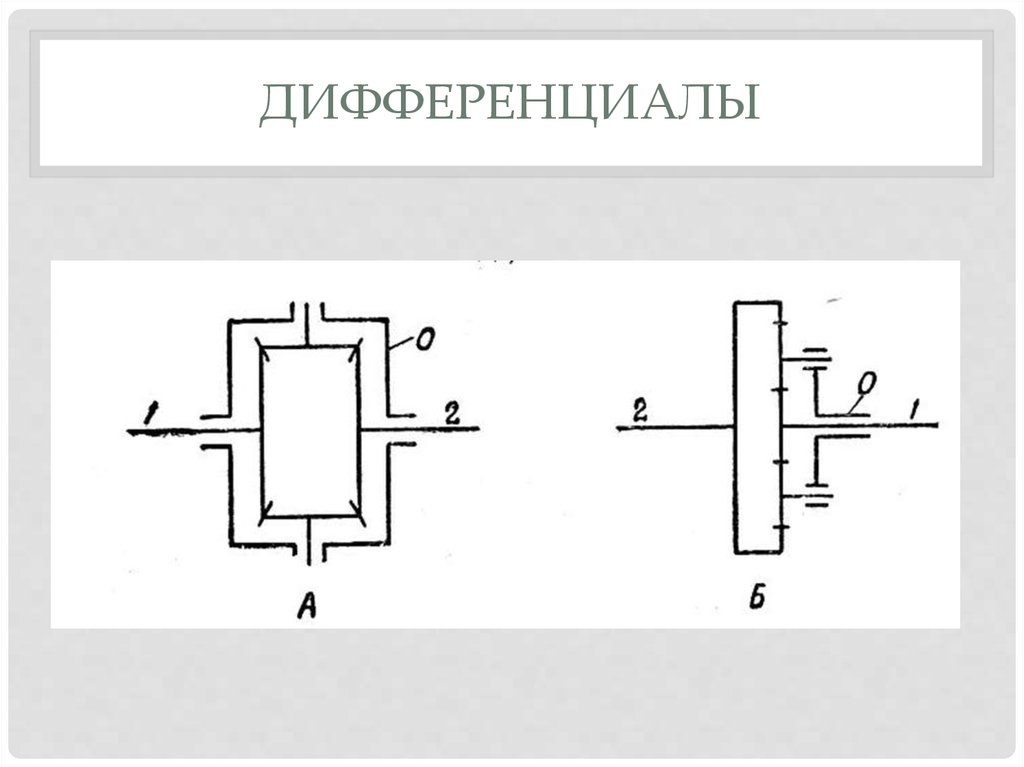 В этой статье представлены основные характеристики компонента дисбаланса дифференциально-парных линий с асимметричной равноудаленной трассировкой и успешно продемонстрирован доминирующий фактор компонента дисбаланса и электромагнитного излучения.
В этой статье представлены основные характеристики компонента дисбаланса дифференциально-парных линий с асимметричной равноудаленной трассировкой и успешно продемонстрирован доминирующий фактор компонента дисбаланса и электромагнитного излучения.
- Публикация:
Радионаука
- Дата публикации:
- Февраль 2015
- DOI:
10.1002/2014РС005507
- Бибкод:
2015RaSc…50..111K
 Гипоидная передача отличается малыми размерами и низким уровнем шума;
Гипоидная передача отличается малыми размерами и низким уровнем шума;