Содержание
Межколесный дифференциал: виды, устройство, принцип работы
Межколесный дифференциал относится к трансмиссионному механизму, который распределяет крутящий момент между валами привода. Кроме того, указанный механизм позволяет вращаться колесам с разными угловыми скоростями. Данный момент особо заметен при проходе поворотов. Кроме того, такая конструкция дает возможность безопасно и комфортно перемещаться по сухому твердому покрытию. В некоторых случаях, при выезде на скользкую трассу или бездорожье, рассматриваемое приспособление может сыграть как стопор для автомобиля. Рассмотрим особенности строения и эксплуатации межколесных дифференциалов.
Описание
Дифференциал предназначен для распределения крутящего момента от карданного вала к ведущим колесным мостам спереди или сзади, в зависимости от разновидности привода. В результате межколесный дифференциал дает возможность проворачиваться каждому колесу без пробуксовки. В этом и заключается прямое назначение механизма.
При прямолинейном перемещении транспорта, когда нагрузка на колеса равномерная с идентичными угловыми скоростями, рассматриваемый агрегат функционирует в роли передаточного отсека. В случае изменения условий движения (буксование, разворот, поворот) нагрузочный показатель изменяется. Полуоси стремятся вращаться с разными скоростными параметрами, возникает необходимость распределение крутящего момента между ними в определенном соотношении. На этом этапе межколесный дифференциал начинает выполнять свою основную функцию – гарантирование безопасности маневров транспортного средства.
Особенности
Схема размещения рассматриваемых автомобильных приспособлений зависит от рабочего ведущего моста:
- На картере коробки переключения передач (передний привод).
- На корпусе ведущего заднего моста.
- Машины с полным приводом оснащаются межколесным дифференциалом на остовах обоих мостов или раздаточных коробках (осуществляют передачу рабочего момента между колесами или мостами, соответственно).

Стоит отметить, что дифференциал на машинах появился не так давно. На первых моделях «самодвижущиеся» экипажи имели плохую маневренность. Проворачивание колес с идентичным угловым параметром скорости приводило к пробуксовке одного из элементов либо потере сцепления с дорожным покрытием. Вскоре инженеры разработали усовершенствованную модификацию устройства, позволяющего нивелировать потерю управляемости.
Предпосылки для создания
Межколесные дифференциалы автомобилей изобрел французский конструктор О. Пеккер. В механизме, предназначенном для распределения вращающегося момента, присутствовали шестерни и рабочие валы. Они служили для трансформации момента кручения от двигателя к ведущим колесам. Несмотря на все преимущества, данная конструкция полностью не решала проблемы с пробуксовкой колес на поворотах. Выражалось это в потере сцепления одного из элементов с покрытием. Особенно выражено момент проявлялся на обледенелых участках.
Буксование в подобных условиях приводило к неприятным происшествиям, что послужило дополнительным стимулом для разработки усовершенствованного приспособления, способного предотвратить занос транспортного средства.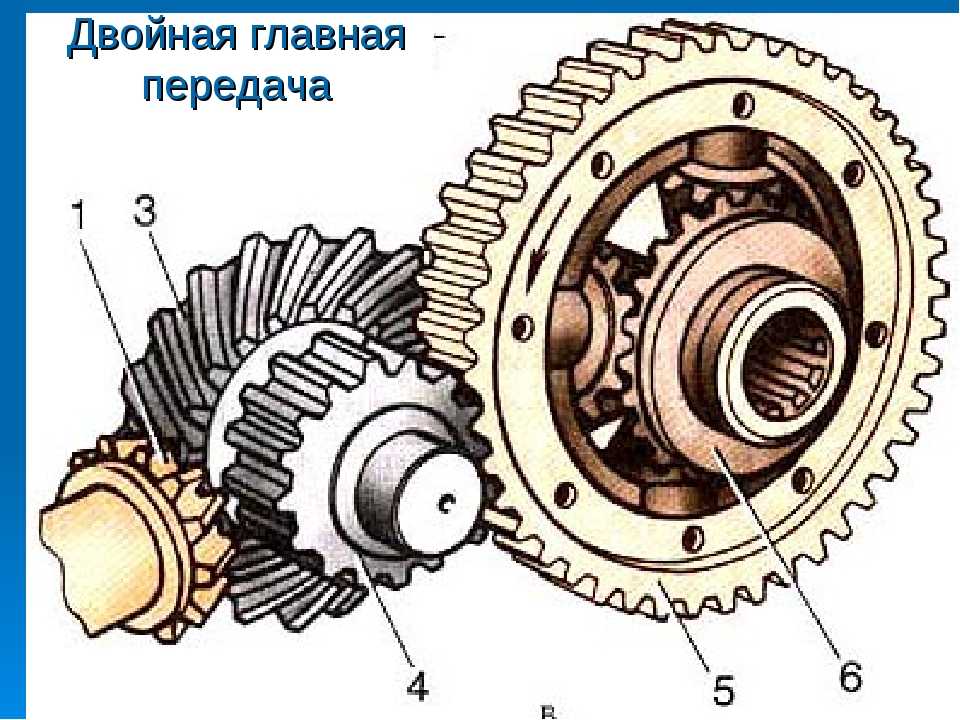 Техническое решение указанной проблемы разработал Ф. Порше, придумавший кулачковую конструкцию, ограничивающую проскальзывание колес. Первыми автомобилями, на которых применялась имитация межколесного дифференциала, стали «Фольксвагены».
Техническое решение указанной проблемы разработал Ф. Порше, придумавший кулачковую конструкцию, ограничивающую проскальзывание колес. Первыми автомобилями, на которых применялась имитация межколесного дифференциала, стали «Фольксвагены».
Устройство
Ограничивающий узел работает по принципу планетарного редуктора. В стандартную конструкцию механизма входят следующие элементы:
- полуосевые шестеренки;
- сопутствующие сателлиты;
- рабочий корпус в виде чаши;
- основная передача.
Остов жестким способом соединен с ведомым зубчатым колесом, которое принимает момент кручения от аналога главной передачи. Чаша через сателлиты трансформирует вращение на ведущие колеса. Разность в скоростных режимах угловых параметров обеспечивается также при помощи сопровождающих шестерен. При этом величина рабочего момента остается стабильной. Задний межколесный дифференциал ориентирован на передачу оборотов на ведущие колеса. Транспортные полноприводные средства оснащаются альтернативными механизмами, воздействующими на мосты.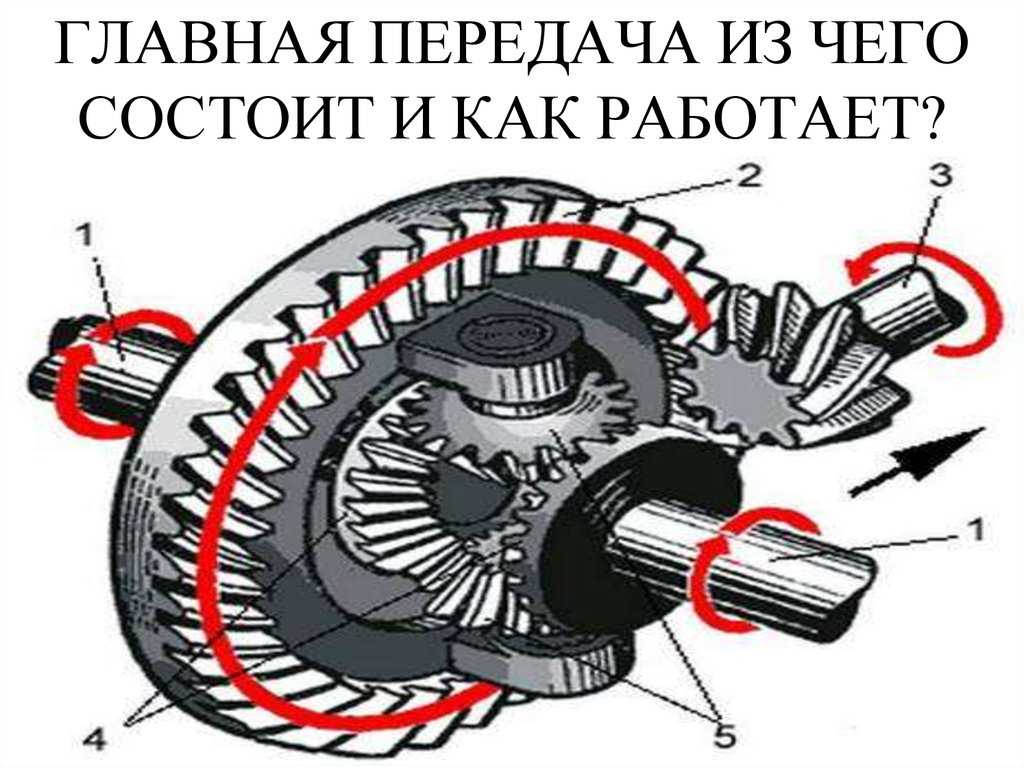
Разновидности
Указанные виды механизмов разделяются по конструкционным признакам, а именно:
- конические версии;
- цилиндрические варианты;
- червячные приспособления.
Кроме того, дифференциалы разделяются по числу зубьев шестеренок полуосей на симметричные и несимметричные версии. По причине оптимальной возможности рассредоточения момента кручения, вторые модификации с цилиндрами монтируются на мосты автомобилей с полным приводом.
Машины с передним или задним ведущим мостом оборудуются симметричными коническими модификациями. Червячная передача универсальна и может агрегировать со всеми типами устройств. Конические агрегаты способны работать в трех конфигурациях: прямолинейным, поворотным и пробуксовочным способом.
Схема работы
При прямолинейном перемещении, электронная имитация блокировки межколесного дифференциала характеризуется равным рассредоточением нагрузки между колесами транспортного средства. При этом наблюдается идентичная угловая скорость, а корпусные сателлиты не вращаются вокруг собственных осей. Они трансформируют момент кручения на полуоси при помощи статичного зубчатого зацепа и ведомой шестеренки основной передачи.
Они трансформируют момент кручения на полуоси при помощи статичного зубчатого зацепа и ведомой шестеренки основной передачи.
На поворотах автомобиль испытывает переменчивое воздействие усилий сопротивления и нагрузки. Параметры распределяются следующим образом:
- Внутреннее колесо меньшего радиуса получает увеличенное сопротивление, по сравнению с наружным аналогом. Повышенный показатель нагрузки обуславливает снижение скорости вращения.
- Внешнее колесо перемещается по большей траектории. При этом увеличение угловой скорости способствует плавному повороту машины, без буксования.
- С учетом указанных факторов, колеса должны обладать различными угловыми скоростями. Сателлиты внутреннего элемента замедляют вращение полуосей. Те же, в свою очередь, через конический зубчатый элемент, повышают интенсивность работы внешнего аналога. При этом момент кручения от основной передачи остается стабильным.
Пробуксовка и курсовая устойчивость
Автомобильные колеса могут получать разный параметр нагрузки, буксуя и теряя сцепление с дорожным покрытием. При этом на один элемент подается чрезмерное усилие, а второй работает «вхолостую». Из-за такой разницы движение автомобиля становится хаотичным или вообще прекращается. Чтобы устранить эти недостатки, используют систему курсовой устойчивости либо ручную блокировку.
При этом на один элемент подается чрезмерное усилие, а второй работает «вхолостую». Из-за такой разницы движение автомобиля становится хаотичным или вообще прекращается. Чтобы устранить эти недостатки, используют систему курсовой устойчивости либо ручную блокировку.
Для того, чтобы момент кручения полуосей выровнялся, следует стопорить действие сателлитов и обеспечить трансформацию оборотов от чаши на нагруженную полуось. Это особенно актуально для межколесных дифференциалов МАЗа и прочих машин повышенной грузоподъемности с полным приводом. Подобная особенность связана с тем, что стоит потерять сцепление в одной из четырех точек, величина крутящего момента устремится к нулю, даже если машина оснащена двумя межколесными и одним межосевым дифференциалом.
Электронный самоблок
Избежать неприятностей, указанных выше, позволяет частичная или полная блокировка. Для этого и применяются самоблокирующиеся аналоги. Они распределяют кручение с учетом разности на полуосях и соответствующих скоростных режимов. Оптимальным способом решения проблемы является оборудование машины электронной блокировкой межколесного дифференциала. Система оснащается датчиками, которые контролируют требуемые показатели во время движения транспортного средства. После обработки полученных данных, процессор выбирает оптимальный режим корректировки нагрузочных и прочих воздействий на колеса и мосты.
Оптимальным способом решения проблемы является оборудование машины электронной блокировкой межколесного дифференциала. Система оснащается датчиками, которые контролируют требуемые показатели во время движения транспортного средства. После обработки полученных данных, процессор выбирает оптимальный режим корректировки нагрузочных и прочих воздействий на колеса и мосты.
Принцип работы данного узла состоит из трех основных стадий:
- В начале проскальзывания ведущего колеса, контрольный блок получает импульсы от индикаторов скорости вращения, после их анализа автоматически принимается решение о способе функционирования. Далее происходит замыкание клапана-переключателя и открывание аналога высокого давления. Помпа узла АБС создает давление в рабочем контуре тормозного цилиндра буксующего элемента. Торможение ведущего проскальзывающего колеса осуществляется за счет повышения давления тормозной жидкости.
- На втором этапе система имитации самоблока удерживает тормозное усилие за счет сохранения давления.
 Действие насоса и пробуксовка колеса прекращается.
Действие насоса и пробуксовка колеса прекращается. - К третьей стадии работы указанного механизма относится завершение проскальзывания колеса с одновременным сбросом давления. Переключатель открывается, а клапан высокого давления закупоривается.
Межколесный дифференциал КамАЗа
Ниже приведена схема указанного механизма с описанием элементов:
1 — Основной вал.
2 — Уплотнитель.
3 — Картер.
4, 7 — Шайбы опорного типа.
5, 17 — Корпусные чаши.
6 — Сателлит.
8 — Индикатор блокировки.
9 — Заливная пробка.
10 — Пневмокамера.
11 — Вилка.
12 — Кольцо-стопор.
13 — Муфта зубчатая.
14 — Блокировочная муфта.
15 — Сливная крышка.
16 — Шестеренка привода среднего моста.
18- Крестовина.
19 — Зубчатая шестерня заднего моста.
20 — Крепежный болт.
21, 22 — Крышка и подшипник.
Безопасность
Межколесный дифференциал предназначен для обеспечения безопасной и комфортной езды на дорогах различного предназначения. Некоторые недостатки рассматриваемого механизма, указанные выше, проявляются при опасном и агрессивном маневрировании по бездорожью. Следовательно, если на машине предусмотрен привод ручного блокиратора, эксплуатировать ее необходимо исключительно в соответствующих условиях. Скоростные машины использовать без указанного механизма весьма затруднительно и небезопасно, особенно на высоких скоростях по шоссе.
Некоторые недостатки рассматриваемого механизма, указанные выше, проявляются при опасном и агрессивном маневрировании по бездорожью. Следовательно, если на машине предусмотрен привод ручного блокиратора, эксплуатировать ее необходимо исключительно в соответствующих условиях. Скоростные машины использовать без указанного механизма весьма затруднительно и небезопасно, особенно на высоких скоростях по шоссе.
Дифференциал на автомобиле — ПРАВИЛЬНОЕ СТРОЕНИЕ МАШИН
Всем механикам с юности памятна картинка со схемой движения автомобиля по кривой, когда его внешние колеса проходят больший путь, чем внутренние. С ее помощью во многих учебниках для водителей разъясняются назначение и принцип действия дифференциала. Часто все сводится к тому, что дифференциал позволяет ведущим колесам вращаться с различными скоростями и, таким образом, обеспечивает нормальное движение автомобиля на поворотах.
Такие разъяснения не то чтобы совсем неправильны, но слишком упрощены и сути работы дифференциала не раскрывают. Конечно, в серьезных книгах все изложено правильно. Там сказано, что назначение межколесного дифференциала на автомобиле состоит в распределении крутящего момента строго поровну между ведущими колесами одного моста, а межмостового дифференциала – в распределении крутящего момента между ведущими мостами, — поровну или в оптимальной пропорции (несимметричный дифференциал).
Конечно, в серьезных книгах все изложено правильно. Там сказано, что назначение межколесного дифференциала на автомобиле состоит в распределении крутящего момента строго поровну между ведущими колесами одного моста, а межмостового дифференциала – в распределении крутящего момента между ведущими мостами, — поровну или в оптимальной пропорции (несимметричный дифференциал).
Эту ситуацию можно считать вполне допустимой для водительских учебников и для популярной литературы, пока объяснения просто не полны и ограничиваются фразами типа:
«Дифференциал – это механизм, у которого ведущие колеса вращаются независимо друг от дружки».
Строго говоря, вращаются они «зависимо», ну да ладно, — что-то похожее на правду сказано, а об остальном ни слова, чтобы не забивать голову людям без специальной подготовки.
Хуже, когда авторы, тиражируют свое неправильное понимание сути работы механизма, как это сделано, например, в книге:
Зеленин С.Ф., Молоков В.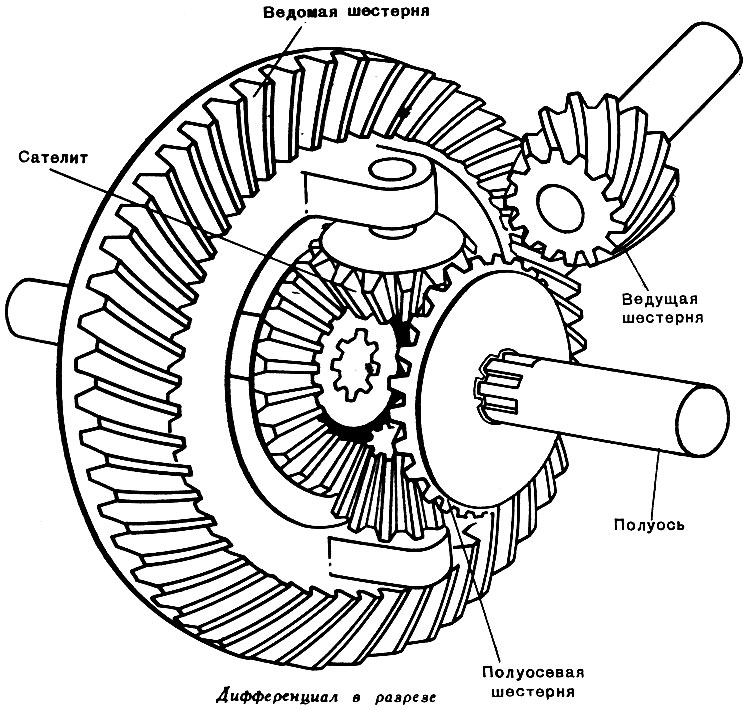 А. Учебник по устройству автомобиля, М., «Русьавтокнига», 2000 г., 80 с. Тираж 15000 экз.
А. Учебник по устройству автомобиля, М., «Русьавтокнига», 2000 г., 80 с. Тираж 15000 экз.
Цитата из этой книги:
«Дифференциал предназначен для распределения крутящего момента между полуосями ведущих колес при повороте автомобиля и при движении по неровностям дороги. Дифференциал позволяет колесам вращаться с разной угловой скоростью и проходить неодинаковый путь без проскальзывания относительно покрытия дороги.
Иными словами 100% крутящего момента, который приходит на дифференциал, могут распределяться между ведущими колесами как 50 х 50, так и в другой пропорции (например, 60 х 40). К сожалению, пропорция может быть и 100 х 0. Это означает, что одно из колес стоит на месте (в яме), а другое в это время буксует (по сырой земле, глине, снегу).
Что поделаешь! Ничто не бывает абсолютно правильным и идеальным, зато данная конструкция позволяет автомобилю поворачивать без заноса, а водителю не менять каждый день напрочь изношенные шины.
Рис. 38 Главная передача с дифференциалом
1 — полуоси; 2 — ведомая шестерня; 3 — ведущая шестерня; 4 — шестерни полуосей; 5 — шестерни-сателиты
Это уже не упрощение, а просто введение в заблуждение читателей. Здесь, кроме второго предложения и иллюстрации, все неправда (в первом предложении нужно вставить слово «поровну», а точку поставить после слова «колес» и т.д.).
Только однажды в учебнике для профтехобразования мне довелось встретить правильное и при этом простое и наглядное разъяснение сути работы дифференциала. Было это давно и помню только, что это был учебник для водителей зерновых комбайнов.
Там читателю предлагалось вообразить, что две полуосевые конические шестерни «развернуты» в две зубчатые рейки, эти рейки лежат на воображаемом столе, а между ними помещен сателлит в виде прямозубой шестерни. Выглядит это примерно так:
Объяснение сути работы дифференциала основано на его конструкции и на третьем законе Ньютона, который гласит: сила действия равна по модулю и противоположна по направлению силе противодействия. На следующем рисунке показано силовое взаимодействие сателлита с рейками, когда движущая сила Д приложена к оси сателлита и этот сателлит толкает обе рейки по столу, причем силы сопротивления движению левой и правой реек Слев и Справ одинаковы (силы трения реек о поверхность воображаемого стола) и каждая из них равна половине общей силы сопротивления С. Силы со стороны сателлита передаются на рейки в точках зацепления зубьев сателлита с зубьями реек. Благодаря равенству сил сопротивления движению Слев и Справ, равны между собой и движущие силы на зубьях сателлита, каждая из которых равна половине движущей силы Д. Поскольку равные силы приложены к двум зубьям сателлита, находящимся на равных расстояниях от его оси, сателлит находится в равновесии и не вращается. Поэтому все три детали движутся прямолинейно в одну сторону и с равными скоростями, а именно с той скоростью, с какой движется ось сателлита и которая задана двигателем.
На следующем рисунке показано силовое взаимодействие сателлита с рейками, когда движущая сила Д приложена к оси сателлита и этот сателлит толкает обе рейки по столу, причем силы сопротивления движению левой и правой реек Слев и Справ одинаковы (силы трения реек о поверхность воображаемого стола) и каждая из них равна половине общей силы сопротивления С. Силы со стороны сателлита передаются на рейки в точках зацепления зубьев сателлита с зубьями реек. Благодаря равенству сил сопротивления движению Слев и Справ, равны между собой и движущие силы на зубьях сателлита, каждая из которых равна половине движущей силы Д. Поскольку равные силы приложены к двум зубьям сателлита, находящимся на равных расстояниях от его оси, сателлит находится в равновесии и не вращается. Поэтому все три детали движутся прямолинейно в одну сторону и с равными скоростями, а именно с той скоростью, с какой движется ось сателлита и которая задана двигателем.
Эта ситуация соответствует установившемуся движению автомобиля по дороге с хорошим сцеплением с дорогой.
Теперь представим, что при своем движении по столу, левая рейка «наехала» на пятно масла. При этом сила сопротивления ее движению (сила трения о стол) уменьшилась, а сила сопротивления движению правой рейки осталась прежней. На какой-то момент равновесие сил на зубьях сателлита нарушается: нагрузка на левый его зуб становится меньше нагрузки, действующей на его правый зуб. Иначе говоря, сателлиту стало легче толкать левую рейку, чем правую. Поэтому он начинает вращаться по часовой стрелке, как это показано на следующем рисунке.
Благодаря вращению сателлита движение правой рейки замедляется, а левая рейка наоборот ускоряется. Затем правая рейка полностью останавливается, а сателлит продолжает вращаться. Его ось продолжает двигаться с той же скоростью, что и прежде, так как эта скорость задана двигателем. Но поскольку правая рейка стоит, вращающийся сателлит обкатывается по ней. В момент, показанный на рисунке правый зуб сателлита стоит на месте, так как «упирается» в зуб неподвижной рейки. Но противоположный, левый зуб сателлита движется в два раза быстрее, чем ось самого сателлита. Все это соответствует ситуации, когда одно из ведущих колес медленно движущегося автомобиля наезжает, например, на обширное пятно льда, а второе остается на сухом покрытии с хорошим сцеплением. То есть машина останавливается и колесо, находящееся на льду, буксует, вращаясь в два раза быстрее, чем прежде, когда оба колеса катились с одинаковой скоростью.
Но противоположный, левый зуб сателлита движется в два раза быстрее, чем ось самого сателлита. Все это соответствует ситуации, когда одно из ведущих колес медленно движущегося автомобиля наезжает, например, на обширное пятно льда, а второе остается на сухом покрытии с хорошим сцеплением. То есть машина останавливается и колесо, находящееся на льду, буксует, вращаясь в два раза быстрее, чем прежде, когда оба колеса катились с одинаковой скоростью.
Строго говоря, о нарушении равновесия сил на зубьях сателлита выше сказано некорректно и только потому, что, как мне кажется, так проще понять происходящее. На самом деле равновесие сил сохраняется всегда, только для его рассмотрения нужно еще учитывать силы, вызывающие ускорение левой рейки и замедление правой. Эти не рассматриваемые нами силы, исчезают с момента полной остановки правой рейки. В этот же момент удвоенная скорость движения левой рейки становится постоянной. И тогда ситуация полностью соответствует следующему рисунку.
Здесь равновесие сил восстановилось, точнее, — исчезли динамические силовые составляющие (те, что вызывали ускорение одной рейки и замедление другой).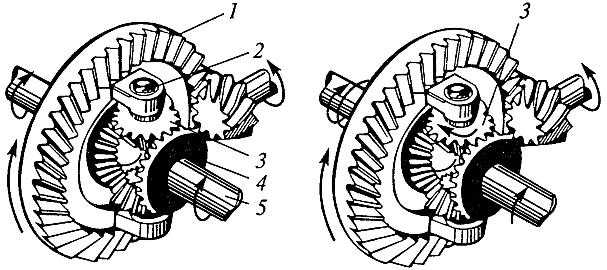 Правая рейка стоит, сателлит вращается, а левая рейка движется равномерно с удвоенной скоростью. Очень важно отметить что, равновесие сил перешло на новый уровень. Теперь равные силы на левом и правом зубьях сателлита стали существенно меньше прежних. В силу третьего закона Ньютона эти силы не могут превысить движущую силу, которую можно приложить к рейке, находящейся на пятне масла, или к колесу, находящемуся на пятне льда. Иными словами, если одно колесо стоит на сухой дороге, а противоположное буксует на льду или в грязи, это вовсе не означает, что 100% крутящего момента передается от двигателя на буксующее колесо, как сказано в упомянутой выше книге. Этот момент всегда и во всех условиях делится дифференциалом поровну между колесами, но он не может быть больше, чем позволяет сцепление одного из колес с дорогой, причем именно того колеса, у которого это сцепление меньше.
Правая рейка стоит, сателлит вращается, а левая рейка движется равномерно с удвоенной скоростью. Очень важно отметить что, равновесие сил перешло на новый уровень. Теперь равные силы на левом и правом зубьях сателлита стали существенно меньше прежних. В силу третьего закона Ньютона эти силы не могут превысить движущую силу, которую можно приложить к рейке, находящейся на пятне масла, или к колесу, находящемуся на пятне льда. Иными словами, если одно колесо стоит на сухой дороге, а противоположное буксует на льду или в грязи, это вовсе не означает, что 100% крутящего момента передается от двигателя на буксующее колесо, как сказано в упомянутой выше книге. Этот момент всегда и во всех условиях делится дифференциалом поровну между колесами, но он не может быть больше, чем позволяет сцепление одного из колес с дорогой, причем именно того колеса, у которого это сцепление меньше.
Только если в этих условиях заблокировать дифференциал, то есть выключить его из работы, тем или иным способом жестко соединив между собой полуоси, можно передать на колесо, стоящее на сухой дороге, подавляющую часть крутящего момента, который может развить двигатель. При этом буксование прекратится, оба колеса будут вращаться с одинаковой скоростью, но подавляющую часть суммарной силы тяги будет обеспечивать только одно из этих колес.
При этом буксование прекратится, оба колеса будут вращаться с одинаковой скоростью, но подавляющую часть суммарной силы тяги будет обеспечивать только одно из этих колес.
Мне кажется, что с помощью модели с зубчатыми рейками можно наглядно объяснить и все прочие режимы работы межколесного дифференциала. Например, ситуацию, иногда возникающую при торможении двигателем. Представим, что автомобиль движется под уклон на сухой дороге с пятнами льда. Водитель тормозит двигателем. В этом случае движущая сила, это сила инерции массы машины. А сила сопротивления движению, это сила, приложенная к осям сателлитов дифференциала со стороны двигателя. Одно из колес наезжает на пятно льда. Сила сцепления этого колеса с дорогой резко уменьшается, и оно начинает вращаться в обратную сторону. Здесь происходит то же самое, что произойдет с рейками если ось сателлита сделать неподвижной, но оставить ему свободу вращения вокруг этой оси, то есть имитировать ситуацию, когда ось сателлита тормозится или удерживается двигателем. Если теперь двинуть вперед одну из зубчатых реек, то сателлит начнет вращаться и заставит вторую рейку двигаться назад. Здесь рейка, движимая вперед, соответствует колесу на сухой дороге, а рейка, движущаяся назад, — колесу, находящемуся на льду и вращающемуся в обратную сторону. На мой взгляд, вращение буксующего колеса в обратную сторону очень наглядно демонстрирует «стремление» дифференциала выполнить свое предназначение и выровнять силы на двух колесах ведущего моста. В данном случае это силы торможения. Благодаря их выравниваю исключается или сильно снижается вероятность заноса автомобиля при таком режиме торможения.
Если теперь двинуть вперед одну из зубчатых реек, то сателлит начнет вращаться и заставит вторую рейку двигаться назад. Здесь рейка, движимая вперед, соответствует колесу на сухой дороге, а рейка, движущаяся назад, — колесу, находящемуся на льду и вращающемуся в обратную сторону. На мой взгляд, вращение буксующего колеса в обратную сторону очень наглядно демонстрирует «стремление» дифференциала выполнить свое предназначение и выровнять силы на двух колесах ведущего моста. В данном случае это силы торможения. Благодаря их выравниваю исключается или сильно снижается вероятность заноса автомобиля при таком режиме торможения.
Можно рассматривать еще многие ситуации, возникающие при работе дифференциала. Но полагаю, что и сказанного достаточно, чтобы убедиться: — межколесный дифференциал всегда делит получаемый от двигателя крутящий момент поровну между двумя колесами одного ведущего моста.
А теперь вернемся к упомянутой в самом начале картинке с автомобилем, движущемся по кривой. Если автомобиль заднеприводной, то получающие одинаковый крутящий момент два задних колеса преобразуют эти крутящие моменты в две одинаковые силы тяги (если шины колес имеют одинаковый диаметр, одинаковое давление накачки и несут одинаковые части веса автомобиля). А две одинаковые силы тяги стремятся толкать автомобиль по прямой. Именно поэтому, водителю при прохождении поворота приходится твердо удерживать рулевое колесо. Строго говоря, дифференциал на таком автомобиле не столько помогает, сколько мешает прохождению поворота. Зато он прямо способствует устойчивости движения по прямой (вместе с углами установки передних колес).
Если автомобиль заднеприводной, то получающие одинаковый крутящий момент два задних колеса преобразуют эти крутящие моменты в две одинаковые силы тяги (если шины колес имеют одинаковый диаметр, одинаковое давление накачки и несут одинаковые части веса автомобиля). А две одинаковые силы тяги стремятся толкать автомобиль по прямой. Именно поэтому, водителю при прохождении поворота приходится твердо удерживать рулевое колесо. Строго говоря, дифференциал на таком автомобиле не столько помогает, сколько мешает прохождению поворота. Зато он прямо способствует устойчивости движения по прямой (вместе с углами установки передних колес).
У переднеприводного автомобиля ситуация несколько иная. Здесь силы тяги также одинаковы на двух колесах, но они «поворачиваются» вместе с поворачиваемыми колесами. Поэтому, например, переднеприводной машине легче выйти из глубокой скользкой колеи: повернутые передние ведущие колеса активно тянут куда нужно. А у заднеприводного, задние ведущие колеса активно толкают машину вдоль колеи.
Здесь рассмотрена лишь малая часть того, что следовало бы водителям знать о работе дифференциала и на это потребовалось много слов и картинок. Так может быть правы те, кто ограничивается пресловутой картинкой с разным пробегом у разных колес на повороте? Может быть. Но полагаю, что следует, если и не вдаваться в пространные разъяснения, то хотя бы просто написать, для чего действительно предназначен этот механизм. А кто захочет дойти до сути, найдет, где об этом почитать. И уж совсем ни к чему пропагандировать собственное неверное понимание этой сути.
Д.Д.
Дифференциальное определение
По
Джеймс Чен
Полная биография
Джеймс Чен, CMT — опытный трейдер, инвестиционный консультант и стратег глобального рынка. Он является автором книг по техническому анализу и торговле иностранной валютой, опубликованных John Wiley and Sons, а также выступал в качестве приглашенного эксперта на CNBC, BloombergTV, Forbes и Reuters среди других финансовых СМИ.
Узнайте о нашем
редакционная политика
Обновлено 24 мая 2022 г.
Рассмотрено
Сомер Андерсон
Рассмотрено
Сомер Андерсон
Полная биография
Сомер Дж. Андерсон является дипломированным бухгалтером, доктором бухгалтерского учета и профессором бухгалтерского учета и финансов, который работает в сфере бухгалтерского учета и финансов более 20 лет. Ее опыт охватывает широкий спектр областей бухгалтерского учета, корпоративных финансов, налогов, кредитования и личных финансов.
Узнайте о нашем
Совет по финансовому обзору
Что такое дифференциал?
Дифференциал — это степень корректировки стоимости или класса физических результатов или их местонахождения, как это разрешено фьючерсным контрактом. Хотя это справедливо не для всех, некоторые фьючерсные контракты допускают дифференциал, также известный как надбавка. Такие фьючерсные контракты позволяют короткой позиции вносить коррективы в место доставки и/или качество или стандарт поставляемого товара или ценной бумаги.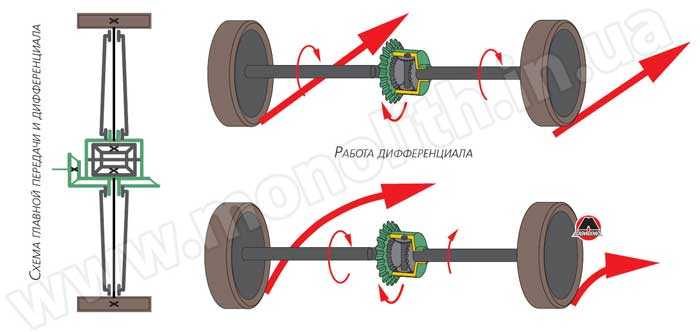 Эти дифференциалы устанавливаются на основе номинальной стоимости или по отношению к центральному местоположению.
Эти дифференциалы устанавливаются на основе номинальной стоимости или по отношению к центральному местоположению.
Ключевые выводы
- Дифференциал — это корректировка качества или стоимости базового актива, указанного в качестве поставки во фьючерсном контракте.
- Фьючерсный контракт устанавливает стандартные условия для базового актива, где дифференциалы включают любые модификации условий контракта.
- Некоторые фьючерсные контракты допускают дифференциал, а другие нет. Если это разрешено, контакты обычно позволяют короткой позиции получить дифференциал.
Объяснение различий
Фьючерсные контракты стандартизированы с точки зрения качества и количества данного товара. Из-за этого фьючерсная цена представляет типичный диапазон качеств товаров и, следовательно, является средней ценой. Цена, зависящая от происхождения и качества любого продукта, не всегда одинакова; она может быть выше или ниже. Премия или скидка физического продукта, дифференциал, представляет собой ценность, которую рынок придает продукту, плюс или минус, в зависимости от цены/качества.
Если будет определено, что оцениваемый товар имеет лучшее качество и цены выше базового уровня, он может иметь повышенную ставку. И наоборот, продукты, которые не соответствуют, по крайней мере, стандартам, установленным базовым сортом, могут быть неприемлемыми. Значительные отклонения от базовой оценки уровня приведут к большим разницам.
Условия контракта определяют дифференциалы, базовый класс и другие условия, связанные с качеством, надбавками или штрафами, и являются фиксированными условиями на большинстве бирж.
Цена и ценовой риск
Исторически сложилось так, что наличная цена и фьючерсная цена товара обычно приближаются друг к другу по мере приближения даты поставки фьючерса. На идеальном рынке или, по крайней мере, на эффективном рынке такая конвергенция довольно распространена. Тем не менее, цена на физический товар почти всегда колеблется и движется вверх и вниз совершенно независимо от фьючерсного рынка. Вот почему дифференциал или дифференциалы вводятся (или вводятся) во фьючерсный контракт. Разница в цене не всегда связана с сортом и качеством товара, но также может отражать местные физические рыночные условия. Вот почему дифференциалы, или дифференциальный риск, являются одним из основных компонентов ценового риска. Другим важным компонентом является базовый ценовой риск, когда фьючерсы на определенный товар растут или падают в целом.
Разница в цене не всегда связана с сортом и качеством товара, но также может отражать местные физические рыночные условия. Вот почему дифференциалы, или дифференциальный риск, являются одним из основных компонентов ценового риска. Другим важным компонентом является базовый ценовой риск, когда фьючерсы на определенный товар растут или падают в целом.
Другие соображения
В большинстве случаев фьючерсные рынки используются для снижения подверженности ценовому риску, поскольку они отражают спрос и предложение на типичный сорт доступных и поставляемых товаров. Однако фьючерсные рынки нельзя использовать для снижения дифференциального риска, поскольку такой риск полностью связан с типом, качеством или происхождением конкретных товаров.
Дифференциальный риск и подверженность риску почти всегда менее велики, чем базовый ценовой риск. По этой причине способность фьючерсного рынка снижать такой риск является важным инструментом управления. Дифференциальный риск никогда не следует игнорировать или списывать со счетов, и анализ исторических дифференциалов для тех же или аналогичных продуктов часто является мудрым решением.
myPhysicsLab Что такое дифференциальное уравнение?
myPhysicsLab Что такое дифференциальное уравнение?
Дифференциальное уравнение может выглядеть довольно устрашающе, с большим количеством причудливых математических символов. Но идея на самом деле довольно проста:
Дифференциальное уравнение показывает, как скорость изменения («дифференциал») одной переменной связана с другими переменными.
Например, симуляция с одной пружиной имеет две переменные: положение блока,
х
, и его скорость,
против
. Каждая из этих переменных имеет дифференциальное уравнение, показывающее, как эта переменная изменяется с течением времени. Дифференциальное уравнение для положения
х
х ‘ = v
где
х ‘
указывает производную от
х
по времени (скорость изменения
х
). Это уравнение говорит
скорость изменения положения равна скорости
Это очевидное утверждение. Подождите, следующее уравнение интереснее:
Подождите, следующее уравнение интереснее:
.
Величина растяжения пружины напрямую связана с положением блока,
х
. Вы можете увидеть подробности на странице моделирования с одной пружиной, но с использованием закона Ньютона.
F = м а
мы можем написать дифференциальное уравнение для скорости
против
как
v ‘ = — к х
где
к
— постоянная пружины (насколько жесткой является пружина). Это уравнение говорит
скорость изменения скорости обратно пропорциональна положению
Например, когда положение равно нулю (т. е. пружина не растянута и не сжата), скорость не меняется. Это имеет смысл, потому что в этот момент пружина не действует.
С другой стороны, когда положение большое (т. е. струна очень сильно растянута или сжата), скорость изменения скорости велика, потому что пружина оказывает большое усилие.
Что такое решение дифференциального уравнения?
Когда вы начинаете изучать математику, вы работаете над поиском решений уравнений, подобных
.
х 2 + 2 х + 1 = 0
, у которого есть решение
х = -1
Для дифференциального уравнения решением является не одно значение, а функция . Задача состоит в том, чтобы найти функцию, различные производные которой соответствуют дифференциальному уравнению за большой промежуток времени. Например,
| х » + 2 х ‘ + х = 0 | (1) |
— дифференциальное уравнение, цель которого — найти функцию
х ( т )
что, когда вы подставляете функцию и ее производные в дифференциальное уравнение, уравнение сохраняет для любого времени
т
.
Общее решение для предыдущего уравнения равно
| x ( t ) = a e − t + b t e − t | (2) |
where
е = 2,71828. ..
..
а также
а , б
являются неопределенными константами. Легко убедиться, что у вас есть решение: просто подставьте решение к дифференциальному уравнению! В нашем примере мы находим первую и вторую производные (см. статью о том, как найти эти производные… это довольно просто!):
| x ‘( t ) = ( b − a ) e − t − b t e − t | (3) |
| x »( t ) = ( a − 2 b ) e − t + b t e − t | (4) |
Теперь подставьте эти уравнения (2), (3) и (4) в левую часть дифференциального уравнения (1) и выполните алгебраические вычисления:
х » + 2 х ‘ + х =
= (( a − 2 b ) e − t + b t e
−
+ 2(( b − a ) e − t − б т д − т )
+ ( a e − t + b t e − t )
= ( a − 2 b + 2 b − 2 a + a ) e − t
+ ( б — 2 б + б ) т д — т
= 0
Следовательно, решение (2) удовлетворяет дифференциальному уравнению (1) при любых значениях
а , б
.

 Действие насоса и пробуксовка колеса прекращается.
Действие насоса и пробуксовка колеса прекращается.